從乘法分配律的直觀解釋說如何學習數學思維

不同于前面的文章，要么是自己講課后的小結，要么是自己讀書時候的領悟，本文是應一位家長朋友的請求而寫。

在我們大人看來很容易理解的乘法分配律，在很多孩子的眼里卻不是很容易理解的事情，甚至有不少五六年級的孩子，對這個運算法則都是似懂非懂，所以有必要寫篇短文來解釋一下這個問題。

先來解釋什么叫做分配律（distributive law）？

首先要說明的是，這里的“分配律”僅限于中小學生課本中所涉及的初等數學部分的知識，不擴展到布爾代數和形式邏輯方面去。如果真要這么解釋，雖然看起來比較嚴謹，但對小學生而言就更加不容易理解了。

“嚴謹”與“精確”相似，只是一個相對的概念，不同的階段用不同的角度和術語來解釋會比較好。有一些數學老師總搞不清這個概念，也把握不了尺度，總以為越抽象的代數證明就越嚴謹。我想，大部分的數學家應該是不贊同這個理念的，至少據我所知，有數學中的莫扎特之稱的陶哲軒就不這么認為。

引述小學課本上的定義：兩個數的和與一個數相乘，可以先把它們分別與這個數相乘，再將積相加，這叫做乘法分配律。

用代數式來表示就是：c×（a＋b）＝c×a＋c×b；

用圖形符號表示就是：■×（▲＋★）＝■×▲＋■×★。

事實上，無論是代數式還是圖形符號，對小朋友而言都不如幾何圖形來得直觀易懂。

先看一道美國四年級的數學學術活動題：64＋64＋64＝8×□。

我看到很多孩子都是把3個64相加得到192，然后再用132除以8得到24。答案對嗎？當然對了，這么簡單的四則運算對中國孩子而言只是小菜一碟。但是很遺憾，出題的人其實不是為了這個24的答案。

這個問題可以怎么去考慮呢？我們知道，64可以寫成8×8，于是64＋64＋64＝8×8＋8×8＋8×8＝8×（8＋8＋8）＝8×24＝8×□，因此得到□＝24。這里其實考的就是乘法的分配率，這樣的計算比大部分孩子先把3個64相加得到192、然后再用132除以8得到24的做法簡單很多，也不容易出錯。

但我發現，很多小朋友對乘法分配率的理解有不同程度的困難，而困難的原因我認為則在于課本的定義和表達式過于抽象。現在我們換個角度來理解這個問題。

我一直不斷鼓勵和訓練孩子們，看到數學表達式要學會通過幾何圖形去進行聯想和構思，看到幾何圖形可以再轉回數學表達式。只要勤加苦練，就能做到來回切換自如，解題時就會變得游刃有余。當年高考，我就是用這樣的方法，在短短的四十分鐘里就做完了整張高考數學試卷，雖然最后沒有得到滿分，但這樣的速度已經讓很多人難以企及了。其實，只要科學有效地進行數學思維訓練，每一個人都是可以做到的。

當我們看到兩個數相乘時，可以聯想到什么呢？矩形的面積。我在多個場合都提到過這個源自幾何之父歐幾里得的理念。因此，回到上題，64＋64＋64＝8×8＋8×8＋8×8本質上其實代表著三個邊長為8的正方形相加，最后可以拼成一個8×（8＋8＋8）＝8×24的長方形。如圖所示：

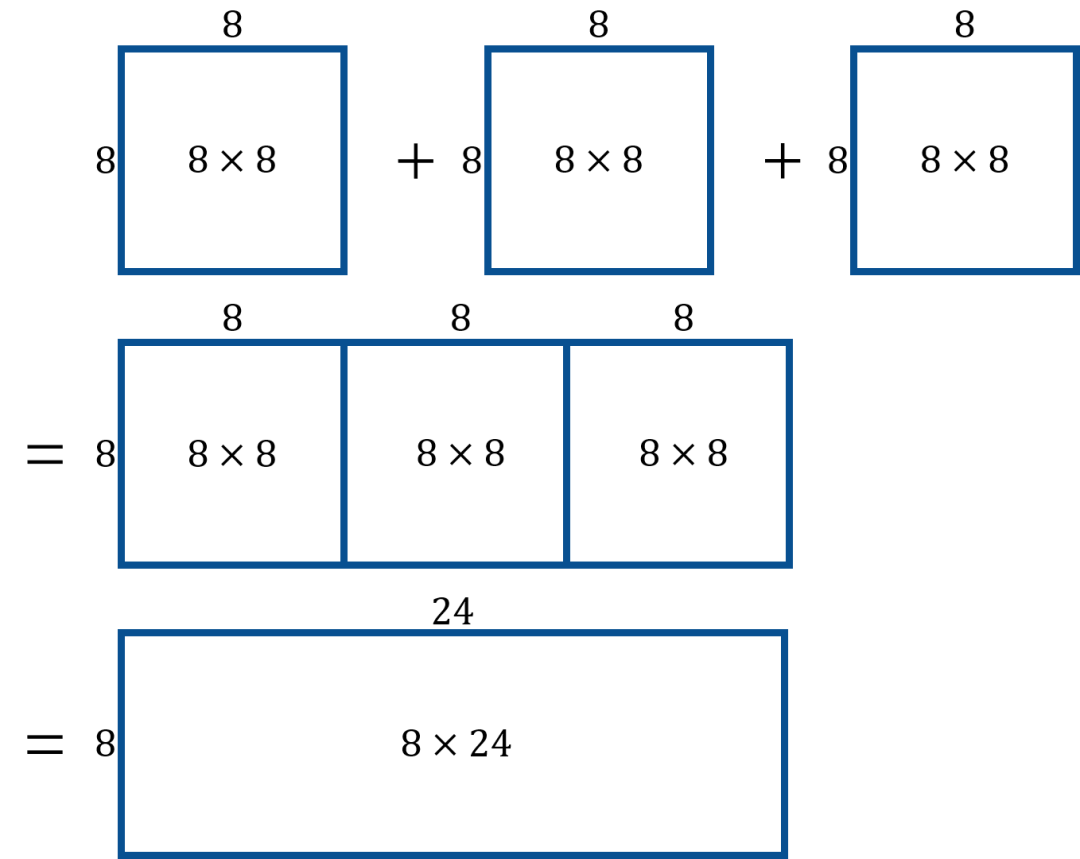
上圖逆向推導其實也是成立的。比如說：

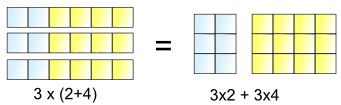
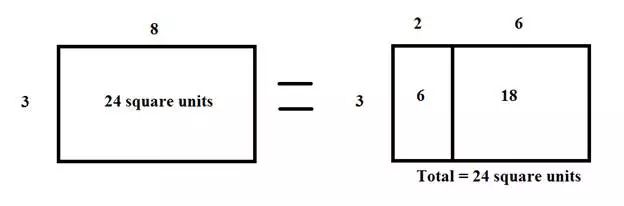
所以，從上面的圖示可以看出，在小學階段的數學問題中，乘法的分配率其實本質上可以理解為矩形的拼接和分割。

進一步，更為復雜的情況可以表示為：

進一步的知識讀者朋友們可以看后面“延伸閱讀”中提到的文章，有很多不同的解釋和應用。

這里，順便再拓展一下，我們再來看一個有點挑戰性的問題：1×1×1＋2×2×2＋3×3×3＋4×4×4＝？

不少小朋友看到問題就是開始死算，很快得到了答案100。對嗎？當然對，和前面的問題一樣，這種計算對中國孩子太簡單。但我的問題是，假如題目改為：1×1×1＋2×2×2＋3×3×3＋…＋100×100×100呢？也進行死算嗎？所以很多孩子其實沒有明白數學究竟學的是什么？

兩個數相乘我們可以理解為矩形的面積，那么三個數相乘呢？聰明的小朋友會說理解成立體圖形。如果會這么思考的孩子說明已經會舉一反三了。確實，可以這么聯想。如圖所示：

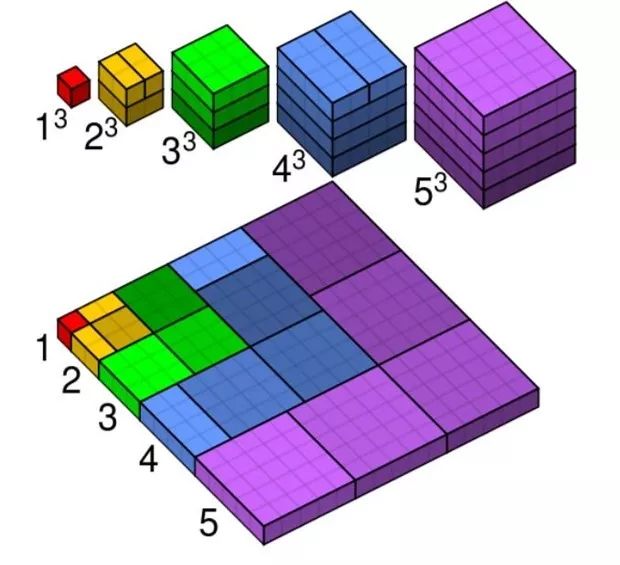
答案就不用過多解釋了吧，這張圖的證明太簡單直白了。不過在這里我想說的是，這個問題還可以換一個角度來思考這個問題。由于從二維平面到三維立體圖形的轉變，數學思維的難度會增加很多，能不能依舊停留在二維平面圖形來思考呢？答案是肯定的。

我們可以把1×1×1看成1個1×1的正方形；把2×2×2看成2個2×2的正方形；把3×3×3看成3個3×3的正方形；……把n×n×n看成n個n×n的正方形。然后拼起來得到下圖：

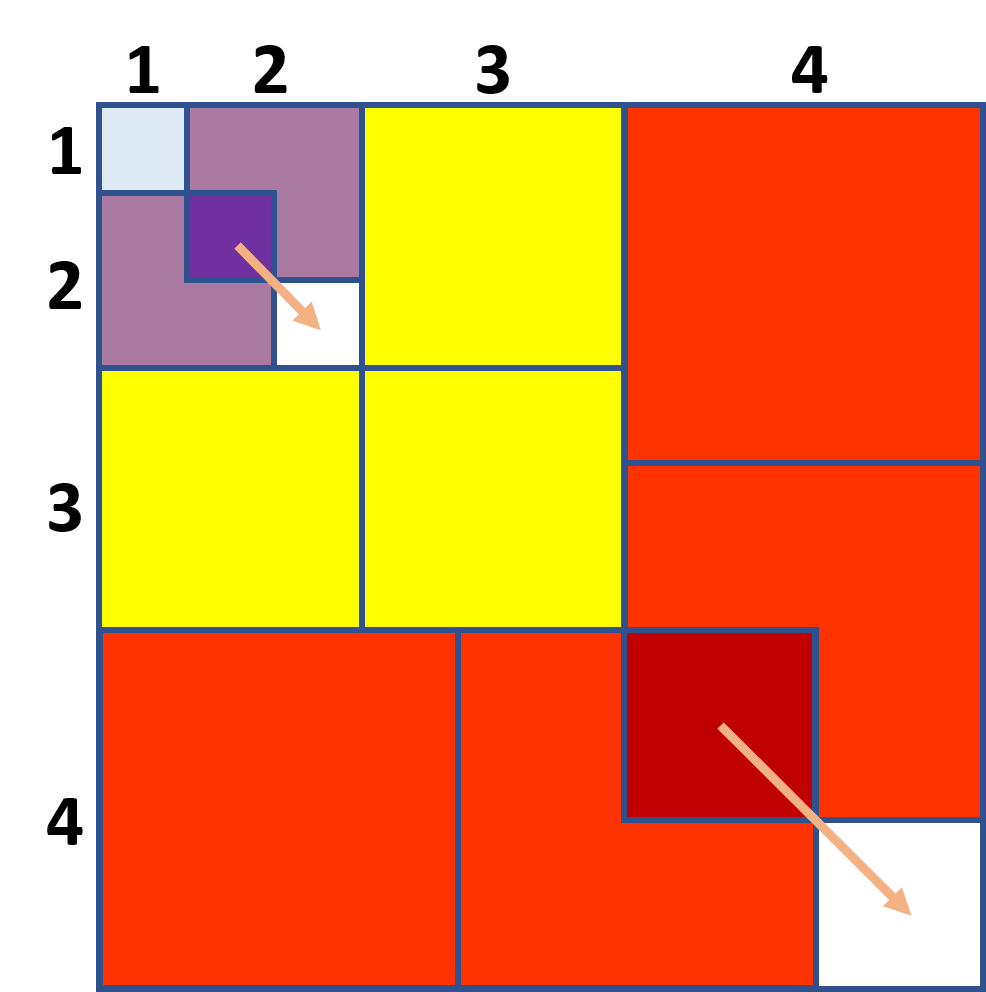
當然，我們還可以這么來看問題：

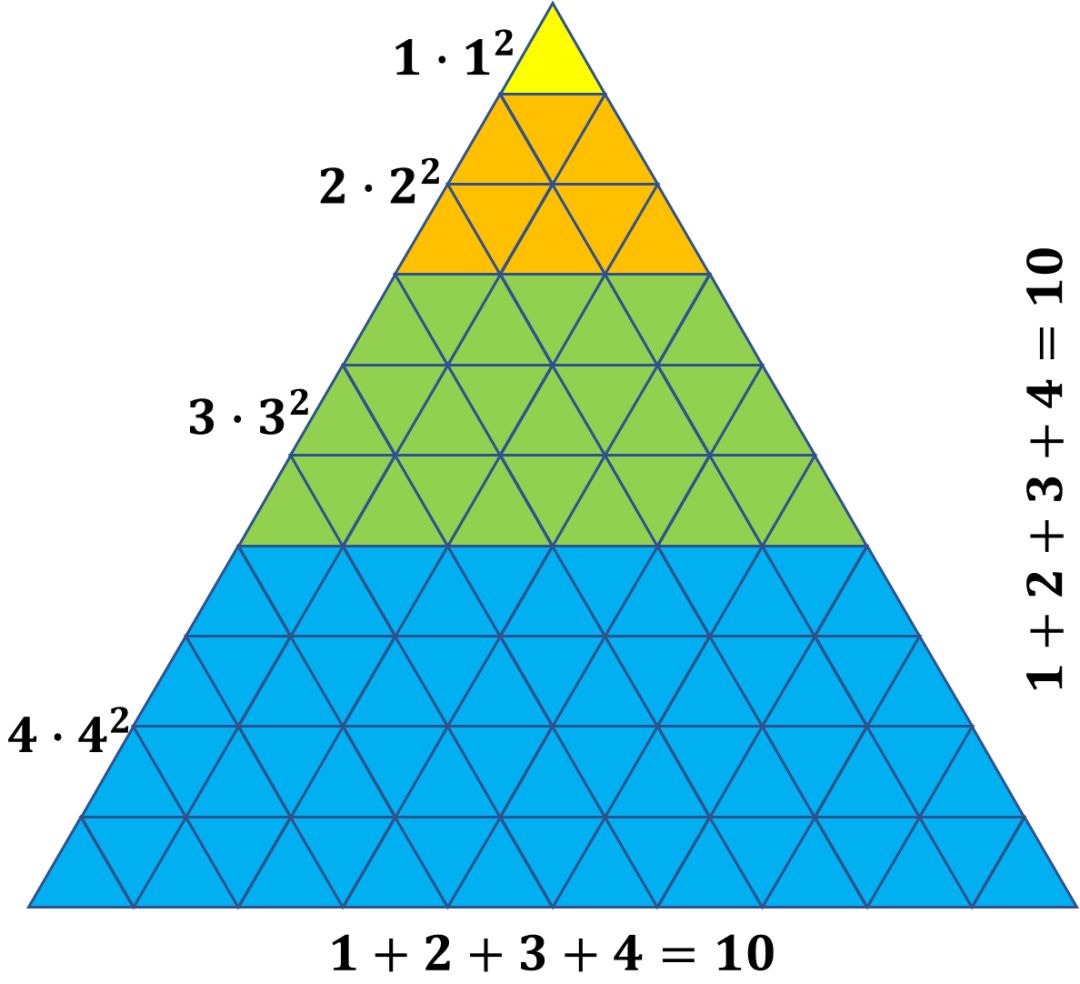
這里需要解釋一下的是左邊的式子n×n2所代表的數學含義。我們發現，在這個圖形里，每一層的三角形數都是奇數，那么從1開始的連續奇數相加有什么性質呢？
還是看圖：

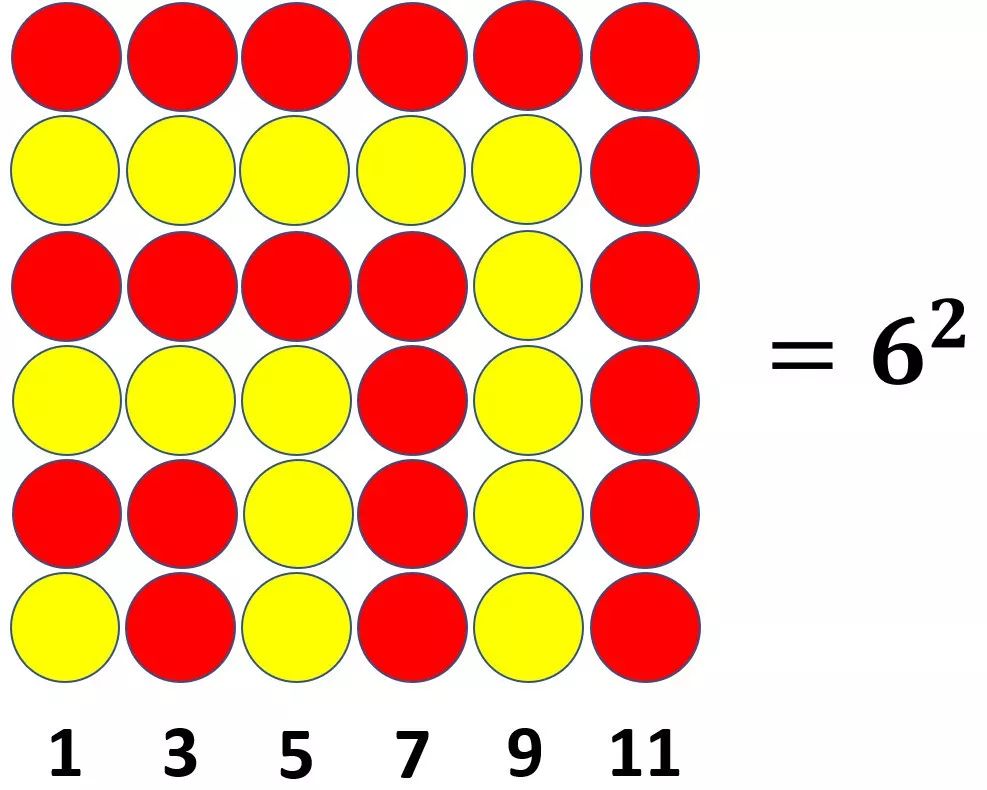
從上圖可以看出，從1開始的連續奇數相加，其和為項數的平方。明白了這一點，我們就可以知道：

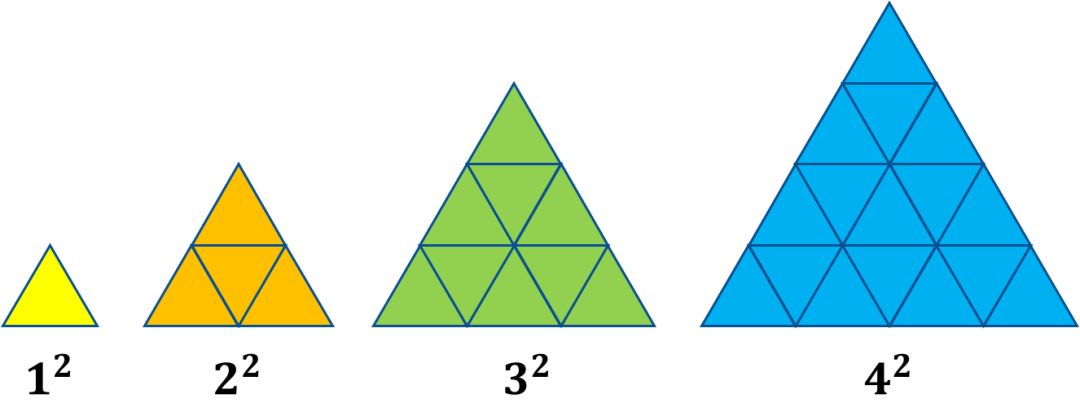
那么上圖其實可以更詳細地表達為：

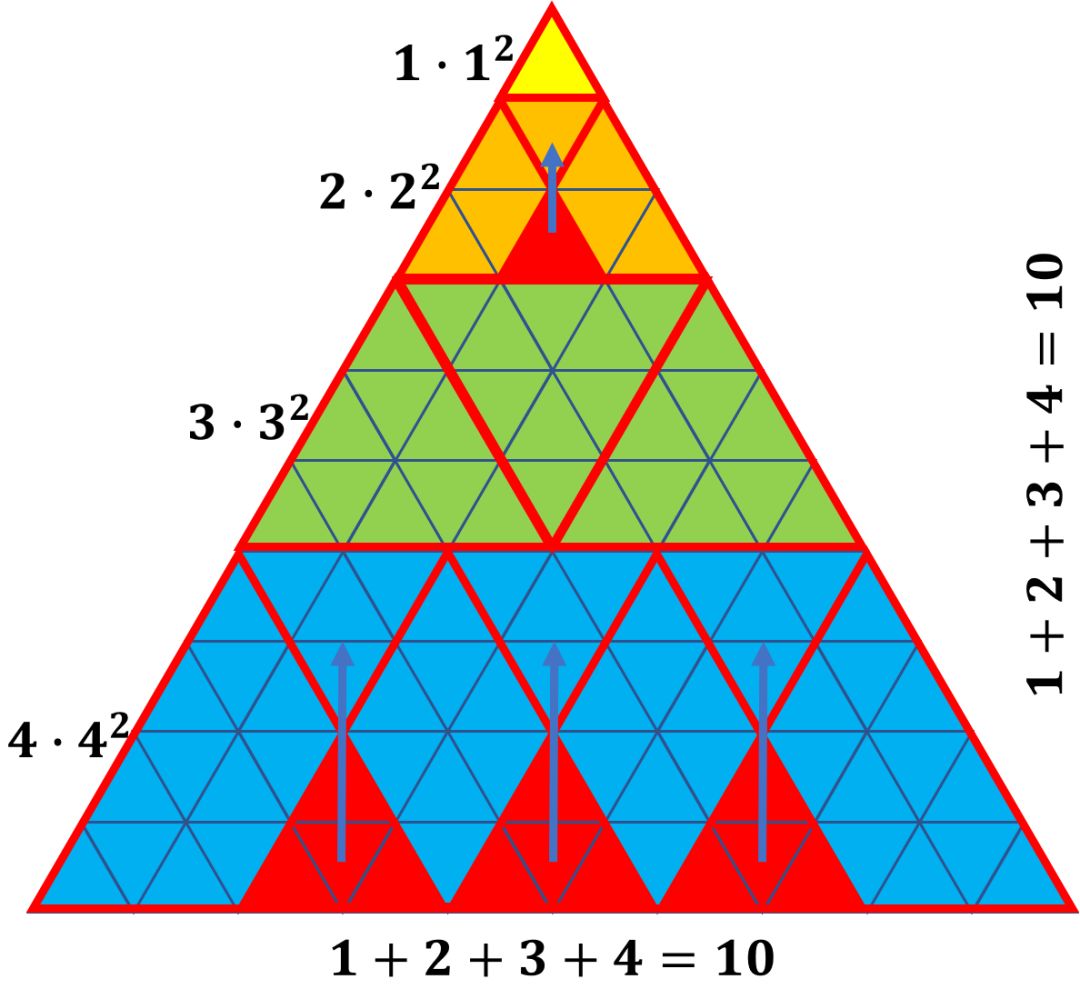
因此，通過幾個角度的直觀證明，我們可以知道：1×1×1＋2×2×2＋3×3×3＋…＋n×n×n＝（1＋2＋3＋…＋n）2。從1開始的連續立方數求和，最后居然變成了一個完全平方數。這里涉及到的證明過程可比計算得到一個簡單的答案有趣多了吧！

學數學，最重要的是學習數學思想和思維方式。這其中就包括觀察發現、歸納類比、空間想象、抽象概括、反思構成、演繹證明等等各種數學思想和能力。
這些才是最有美感的東西，而不是那些個簡單重復的計算，答案固然重要，但那只是水到渠成的結果。很多孩子似乎都搞不清這個問題的重要性，當然責任主要在于我們很多數學教育工作者們的教育導向出了很嚴重的問題。