- 翰林提供學(xué)術(shù)活動(dòng)、國(guó)際課程、科研項(xiàng)目一站式留學(xué)背景提升服務(wù)!
- 400 888 0080
AP統(tǒng)計(jì)5分必考點(diǎn)梳理,省時(shí)又高效!
概述
統(tǒng)計(jì)按照大綱共分為四部分,分別是描述統(tǒng)計(jì)、抽樣方法、概率論、統(tǒng)計(jì)推斷。
(1) Exploring Data:?Describing patterns anddepartures from patterns
(2) Sampling and Experimentation:?Planningand conducting a study
(3) Anticipating Patterns:?Exploring randomphenomena using probability and simulation
(4) Statistical Inference:?Estimatingpopulation parameters and testing hypotheses
描述統(tǒng)計(jì)數(shù)據(jù)(data)分為定性數(shù)據(jù)(qualitative or categorical?data)與定量數(shù)據(jù)(quantitativedate)。
定性數(shù)據(jù):按照類別進(jìn)行劃分,展示對(duì)象的屬性;
定量數(shù)據(jù):展示對(duì)象的數(shù)值特征。
圖(graph):分為bar chart, pie chart, dotplot, stemplot, histogram, boxplot
| Quality | Quantity | |
| Bar chart | YES | NO |
| Pie chart | YES | NO |
| Stemplot | NO | YES |
| Dotplot | YES | YES |
| Histogram | NO | YES |
| Boxplot | NO | YES |
通過圖形可以看出數(shù)據(jù)的分布特征(1)對(duì)稱(symmetric)
(2)偏態(tài)(skewed)
左偏(skewed to the left)
右偏(skewed to the right)
(3)集中趨勢(shì)
(4)異常值
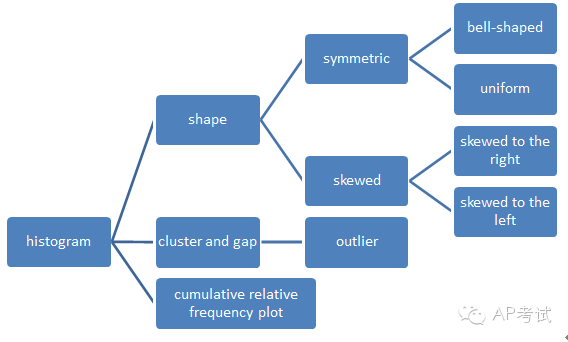
histogram的畫法(1)以個(gè)數(shù)作為高度
(2)以百分比作為高度
(3)以百分比作為面積。
概率密度(probability density function, pdf)描繪以百分比作為面積的histogram的曲線。累積分布(cumulative distribution function, cdf)以小于等于該數(shù)的數(shù)據(jù)所占百分比作為該數(shù)的縱坐標(biāo)繪制出的曲線。數(shù)字特征(numerical value)(1)描述集中趨勢(shì)
(2)描述離散趨勢(shì)
(3)描述位置
(4)標(biāo)準(zhǔn)化變量(z-score)
| Center | Mode | Mean | Median | |
| Spread | Range | Interquartile range | Variance | Standard deviation |
| Position | Simple ranking | Percentile ranking | ||
| Z-score |
眾數(shù)(mode)一組數(shù)據(jù)中出現(xiàn)次數(shù)最多的數(shù)。平均數(shù)(mean)數(shù)據(jù)求和后除以數(shù)據(jù)個(gè)數(shù)。數(shù)據(jù)的排序方式(從小到大)有兩種(1)簡(jiǎn)單排序(simple ranking):
第一、第二、第三等等
(2)百分位排序(percentile ranking):
某個(gè)數(shù)的百分位值等于小于該數(shù)的數(shù)據(jù)個(gè)數(shù)占整體的百分比。
將一組數(shù)據(jù)排序后,可得到
a.最小值(minimum)、最大值(maximum)
b.極差(range):最大值與最小值的差,max-min
c.中位數(shù)(median):排序后處于中間位置的數(shù)
d.四分位數(shù)(quartile):
位于25%、75%的數(shù),記為Q1、Q3
(1).四分位差(interquartile range, IQR):兩個(gè)四分位數(shù)的差值,IQR=Q3-Q1
(2).判斷某個(gè)數(shù)是否為異常值(outlier),可用Q1-1.5IQR和Q3+1.5IQR作為標(biāo)準(zhǔn)進(jìn)行衡量,如果該數(shù)超出這個(gè)范圍則可認(rèn)定為異常值。
(3)箱線圖(boxplot):
剔除異常值后取最小值、Q1、中位數(shù)、Q3、最大值這五個(gè)數(shù),最小值最大值作為兩個(gè)端點(diǎn),Q1、中位數(shù)、Q3作為三條線畫出的圖形。將異常值以散點(diǎn)的形式標(biāo)注在最小值左側(cè)和最大值右側(cè)。
方差(variance)與標(biāo)準(zhǔn)差(standard deviation):衡量數(shù)據(jù)與平均值偏離程度平方和的平均值。
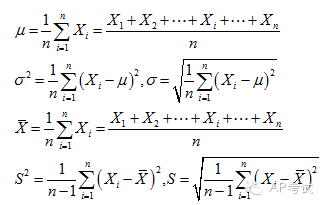
這里需要注意的是,如果計(jì)算的是總體的方差和標(biāo)準(zhǔn)差,用1/n來求平均;如果計(jì)算的是樣本的方差和標(biāo)準(zhǔn)差,用1/(n-1)來求平均。
標(biāo)準(zhǔn)化變量(z-score):計(jì)算方式是將原始數(shù)據(jù)減去平均數(shù)之后再除以標(biāo)準(zhǔn)差,用它可以展示不同度量單位數(shù)據(jù)的偏離程度。
![]()
二維數(shù)據(jù)
二維定量數(shù)據(jù)
研究?jī)蓚€(gè)變量的關(guān)系
散點(diǎn)圖(scatterplot)以一個(gè)變量作為橫坐標(biāo)、另一個(gè)變量作為縱坐標(biāo)繪制出的圖形,以散點(diǎn)的形式表現(xiàn)在坐標(biāo)軸中。變量選用單位不同,會(huì)造成圖形有差異。相關(guān)系數(shù)(linear correlation coefficient)衡量?jī)蓚€(gè)量之間線性關(guān)系的指標(biāo),介于-1和1之間,負(fù)數(shù)代表兩個(gè)變量之間是反向變化的,正數(shù)代表兩個(gè)變量之間是同向變化的,越靠近0代表線性關(guān)系越弱,越靠近-1和1代表線性關(guān)系越強(qiáng)。它只能衡量線性關(guān)系,不能衡量非線性關(guān)系;只反應(yīng)關(guān)系,不代表因果。回歸(regression)尋找代表變量之間關(guān)系的數(shù)學(xué)表達(dá)式。線性回歸假定變量之間存在一次函數(shù)的關(guān)系(形如y=kx+b)。此函數(shù)在坐標(biāo)系中圖像是一條直線,因此稱作線性回歸。殘差(residual)真實(shí)值與估計(jì)值之間的差。殘差圖(residual plot)以一個(gè)變量作為橫坐標(biāo)、該變量所對(duì)應(yīng)的殘差為縱坐標(biāo)繪制出的圖形。若兩變量之間存在線性關(guān)系,則殘差圖應(yīng)為無規(guī)則的散點(diǎn)。最小二乘法(least square)利用殘差平方和最小求出直線斜率與截距(k和b)的方法。線性化(linearity)將非線性關(guān)系轉(zhuǎn)換為線性關(guān)系的方法,常用有對(duì)數(shù)變換、指數(shù)變換等。
抽樣方法總體(population):
研究對(duì)象的全體。
樣本(sample):
總體中的一部分。
參數(shù)(parameter):
描述總體特征的指標(biāo),一般用希臘字母表示。
統(tǒng)計(jì)量(statistics):
描述樣本特征的指標(biāo),一般用拉丁字母表示。
普查(census):
對(duì)總體中的每一個(gè)個(gè)體都進(jìn)行研究。
抽樣(sample):
對(duì)總體中的部分個(gè)體進(jìn)行研究。
實(shí)驗(yàn)法(experiment):
對(duì)目標(biāo)群體進(jìn)行干預(yù)而得到數(shù)據(jù)。
觀察法(observation):
不對(duì)目標(biāo)群體進(jìn)行干預(yù)而得到數(shù)據(jù)。
實(shí)驗(yàn)組(treatment group):
對(duì)該組中的個(gè)體進(jìn)行干預(yù)。
對(duì)照組(control group):
不對(duì)該組中的個(gè)體進(jìn)行干預(yù)。
影響因子(factor):
會(huì)對(duì)實(shí)驗(yàn)對(duì)象產(chǎn)生影響
變量混淆(confounded):
無法分離因子的影響
協(xié)同作用(common response):
多個(gè)因子共同造成影響
安慰劑(the placebo effect):
心理作用導(dǎo)致的變化
單盲試驗(yàn)(single blinding):
實(shí)驗(yàn)者知曉每一個(gè)體是否受到預(yù)先設(shè)置的干預(yù),而被實(shí)驗(yàn)者不知曉。
雙盲試驗(yàn)(double blinding):
實(shí)驗(yàn)者與被實(shí)驗(yàn)者都不知曉每一個(gè)體是否受到預(yù)先設(shè)置的干預(yù)。
簡(jiǎn)單隨機(jī)抽樣(simple random sampling):
隨機(jī)地從總體中選取個(gè)體,每個(gè)個(gè)體被選到的概率是相等的。
系統(tǒng)抽樣(systematic sampling):
首先將總體中的個(gè)體編號(hào)、排序,而后按照固定步長(zhǎng)進(jìn)行抽樣。
分層抽樣(stratified sampling):
首先將總體中的個(gè)體按照某一特征或標(biāo)準(zhǔn)劃分為不同的層(strata),而后從每層中進(jìn)行抽樣。特征是每個(gè)層中的個(gè)體具有相似性。
整群抽樣(cluster sampling):
首先將不同特征的個(gè)體劃為分一個(gè)群(cluster),而后從每個(gè)群中進(jìn)行抽樣。特征是每個(gè)群具有多樣性。
概率頻數(shù)(frequency):
某一結(jié)果出現(xiàn)的次數(shù)。
頻率(relative frequency):
某一結(jié)果出現(xiàn)的次數(shù)占實(shí)驗(yàn)次數(shù)的百分比。
概率(probability):
某一結(jié)果出現(xiàn)可能性的大小,介于0和1之間。不可能事件(impossible event)的概率是0,必然事件(certain event)的概率是1,但反之不正確,概率為0的事件不一定是不可能事件,也有可能發(fā)生,概率為1的事件也可能不發(fā)生。
大數(shù)定律(the law of large numbers):
實(shí)驗(yàn)次數(shù)越大,頻率越穩(wěn)定,且取決于事件本身的概率。
基本公式:
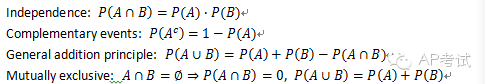
條件概率(conditional probability):
給定某一事件發(fā)生的條件下,另一事件發(fā)生的概率。
隨機(jī)變量(random variable):
該變量的取值取決于實(shí)驗(yàn)的結(jié)果。
離散型(discrete):
隨機(jī)變量的取值是一個(gè)一個(gè)的。
連續(xù)型(continuous):隨機(jī)變量的取值是連續(xù)不間斷的。
分布(distribution):
實(shí)驗(yàn)結(jié)果出現(xiàn)的規(guī)律。
均值(mean)與方差(variance):

二項(xiàng)分布(binomial distribution):
將具有兩個(gè)結(jié)果的實(shí)驗(yàn)重復(fù)多次,求其中某一結(jié)果出現(xiàn)次數(shù)的概率。
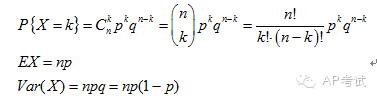
幾何分布(geometric distribution):
將具有兩個(gè)結(jié)果的實(shí)驗(yàn)重復(fù)多次,求其中某一結(jié)果首次出現(xiàn)時(shí)實(shí)驗(yàn)次數(shù)的概率。
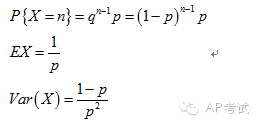
正態(tài)分布(normal distribution):
代表常規(guī)現(xiàn)象出現(xiàn)次數(shù)多、極端現(xiàn)象出現(xiàn)次數(shù)少這樣一種規(guī)律。
標(biāo)準(zhǔn)正態(tài)分布(standard normal distribution):
均值為0、方差為1的正態(tài)分布。
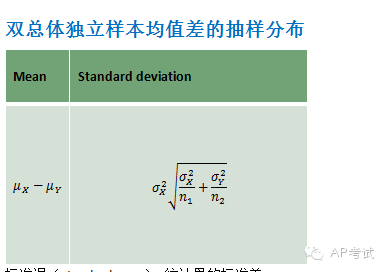
抽樣分布(sampling distribution):
多次抽樣后,樣本統(tǒng)計(jì)量的分布規(guī)律。
標(biāo)準(zhǔn)誤(standard error):
統(tǒng)計(jì)量的標(biāo)準(zhǔn)差。
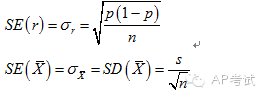
單總體樣本比例的抽樣分布

統(tǒng)計(jì)推斷
參數(shù)估計(jì)(estimation):
利用統(tǒng)計(jì)量去預(yù)測(cè)參數(shù)。
區(qū)間估計(jì)(interval):
給出參數(shù)的范圍。
置信水平(confidence level):
對(duì)參數(shù)多次進(jìn)行估計(jì)得到多個(gè)區(qū)間,其中區(qū)間中包含真實(shí)參數(shù)的次數(shù)占估計(jì)次數(shù)的比例。
單總體比例區(qū)間估計(jì):
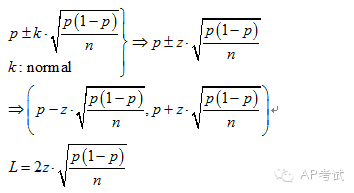
雙總體比例差區(qū)間估計(jì):
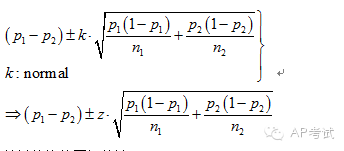
單總體均值區(qū)間估計(jì):
此時(shí)需考慮總體方差是否已知,(1)若已知?jiǎng)t使用正態(tài)分布進(jìn)行估計(jì),(2)若未知?jiǎng)t使用t分布進(jìn)行估計(jì)。
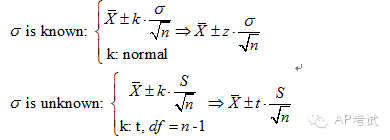
雙總體均值差區(qū)間估計(jì):
此時(shí)需考慮總體方差是否已知
(1)若已知?jiǎng)t使用正態(tài)分布進(jìn)行估計(jì)
(2)若未知
a.總體方差不等(pooled=no)
b.總體方差相等(pooled=yes),則使用t分布進(jìn)行估計(jì),但所用自由度與方差皆不相同。
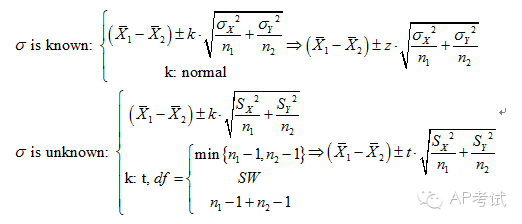
假設(shè)檢驗(yàn)(hypothesis test):
利用統(tǒng)計(jì)量對(duì)參數(shù)的真?zhèn)芜M(jìn)行檢驗(yàn)。
原假設(shè)(null hypothesis):
待檢驗(yàn)參數(shù)。
備擇假設(shè)(alternative hypothesis):
當(dāng)原假設(shè)被拒時(shí)所接受的假設(shè)。
根據(jù)備擇假設(shè)形式的不同,分為雙尾檢驗(yàn)(two tailed)和單尾檢驗(yàn)(one tailed)
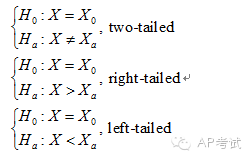
p值(p-value):
當(dāng)原假設(shè)為真的時(shí)候得到此樣本結(jié)果以及比此樣本結(jié)果更極端結(jié)果的概率。p值越小,拒絕原假設(shè)的可能性越大。
第一類錯(cuò)誤(type I error):原假設(shè)為真時(shí)卻拒絕原假設(shè)。犯此錯(cuò)誤的概率為顯著性水平(significance level)。
第二類錯(cuò)誤(type II error):原假設(shè)為假時(shí)卻沒有拒絕原假設(shè)。不犯此類錯(cuò)誤的概率成為檢驗(yàn)的power(power of the test)。
在樣本容量(sample size)固定的條件下,兩類錯(cuò)誤為此消彼長(zhǎng)的關(guān)系,若想同時(shí)降低兩類錯(cuò)誤,只能提升樣本容量。
單總體比例檢驗(yàn):

雙總體獨(dú)立樣本比例差檢驗(yàn):
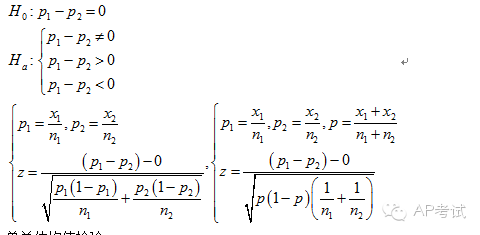
單總體均值檢驗(yàn):
此時(shí)需考慮總體方差是否已知
(1)若已知?jiǎng)t使用正態(tài)分布進(jìn)行檢驗(yàn)
(2)若未知?jiǎng)t使用t分布進(jìn)行檢驗(yàn)。
雙總體均值差檢驗(yàn):
此時(shí)需考慮總體方差是否已知
(1)若已知?jiǎng)t使用正態(tài)分布進(jìn)行檢驗(yàn)
(2)若未知
a.總體方差不等(pooled=no)
b.總體方差相等(pooled=yes),則使用t分布進(jìn)行估計(jì),但所用自由度與方差皆不相同。
卡方檢驗(yàn)(Chi-square)
擬合優(yōu)度檢驗(yàn)(goodness of fit):利用樣本信息來檢驗(yàn)總體是否符合某一分布。
獨(dú)立性檢驗(yàn)(independence):檢驗(yàn)?zāi)骋环诸惤Y(jié)果是否受另一分類影響。
計(jì)算器命令列表
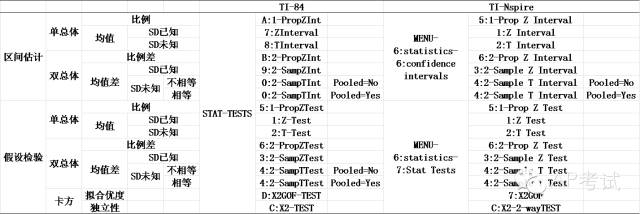

最新發(fā)布
? 2025. All Rights Reserved. 滬ICP備2023009024號(hào)-1









