- 翰林提供學術活動、國際課程、科研項目一站式留學背景提升服務!
- 400 888 0080
一道AMC8真題的解法分析和對比
當前盛行的“刷題”模式,是病態的數學教育的一種具體形式。它在加強學生的應試解題能力的同時,極大地削弱了數學研究的能力。長此以往,將危及數學教育的根基。
在前兩篇文章《一道AMC8真題的解法分析和對比》和《一道AMC8真題的解法分析和對比(續)》里,我對一道AMC8真題給出了幾個解法并做了一些對比和分析。使用這幾個解法中的任意一個,都可以完成這道題的作答。然而,以解決一個數學問題的標準,僅僅做到這一步還遠遠不夠。
本文將討論兩個問題。
第一,這幾個解法給出的答案,實際上只是“某個(跟“胖十字形”有8個交點的)正方形”的面積。但是,我們并沒有確定,這個正方形就是所有正方形中面積最大的那個。
第二,如果在任意形狀的“十字形”內部作正方形,最大面積都是唯一確定的,那么其數值跟“十字形”的形狀數據之間是否有確定的關聯性?換句話說,是否有計算最大面積值的計算公式(公式中只包含跟“十字形”的形狀有關的數量)?
為敘述方便,下面稱這個“十字形”為M。
先不考慮“面積最大”的要求,只是在M中作正方形,可以作出很多不同的正方形。這些正方形有的是“正著”擺的,有的是“斜著”擺的。對于后者,我們可以認為是把前者旋轉一個角度得到的。
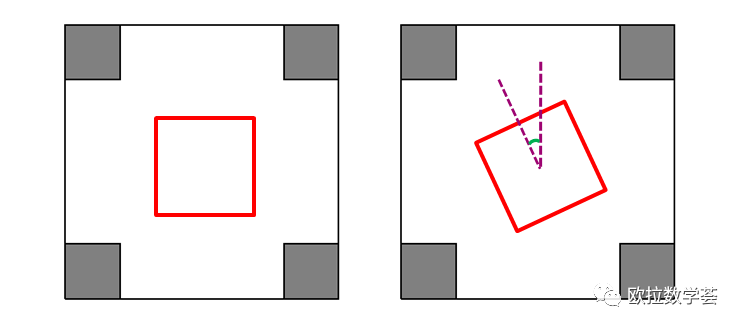
結論一:每個正方形都由三個要素唯一確定:中心點O,旋轉角的大小s,邊長L。
要根據這“三要素”作出唯一確定的正方形,我們可以先標出中心點,再根據旋轉角過這個中心點作一條軸線,最后根據邊長大小把正方形畫出來。
為了探索正方形的面積最大可以達到多大,在選定中心點以及旋轉的角度后,我們再逐漸增加邊長,直到觸碰到邊界為止。
顯然,在選定中心點位置O和旋轉角度s后,按上述方法確定的“最大面積”的正方形是唯一的。我們記這個正方形為Q(O,s)。
現在我們調整一下順序,先取定旋轉角度s。然后,每選擇一個中心點位置O,就得到相應的唯一“最大面積”正方形Q(O,s)。
結論二:對于給定的旋轉角度s,在所有正方形Q(O,s)中,O位于M的中心點的那個正方形Q(O,s)是面積最大的。
從直觀上不難理解這個結論。證明思路如下:如果選定的O不是位于M的中心點,那么在作出Q(O,s)后,把Q(O,s)平移,使得它的中心點移動到M的中心點位置。這個新的正方形仍然在M內,而且在保持中心點和旋轉角度不變的情況下,邊長還有可能再增大。
根據結論二,我們要尋找的面積最大的正方形,其中心點必定位于M的中心點。因此,只需要再比較不同旋轉角度下的“最大面積”正方形的面積。
盡管旋轉角度的取值范圍是從0度到360度,但根據對稱性,我們只需考慮s在0度到45度之間的情形。下面具體計算Q(O,s)的邊長。
記初始的大正方形邊長為a,四個角上切去的正方形邊長為b。注意到每個Q(O,s)都不能再繼續“擴張”了,所以它們要么是邊觸碰到了M的凹頂點(如下圖中的四個紫色點),要么是角觸碰到了M的邊,也可能兩種觸碰同時發生。
下面先考慮第一種觸碰的情形。
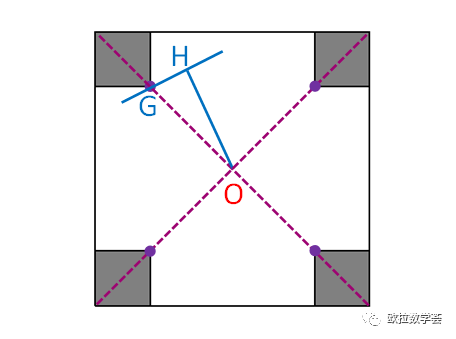
設GH是Q(O,s)的一條邊,其中OH垂直于GH。
可知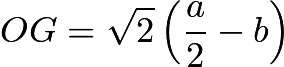 ,
,![]() 。
。
因為![]() ,
,
所以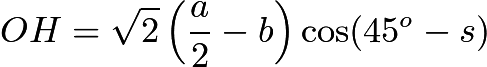 。
。
注意到OH是Q(O,s)邊長的一半,所以Q(O,s)的邊長不大于OH的兩倍,即![]() 。
。
接下來考慮第二種觸碰的情形。
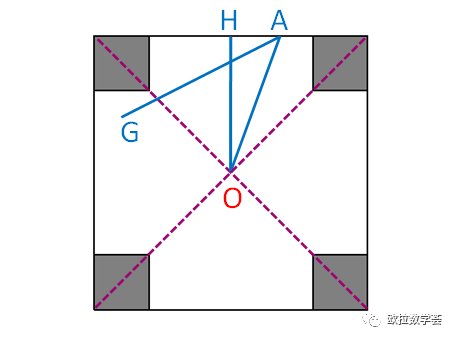
設A是Q(O,s)的其中一個頂點,且位于M的一條邊上。作OH垂直于M的這條邊,垂足為H。
則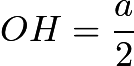 ,
,![]() 。
。
所以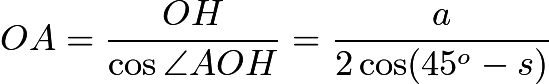 。
。
注意到Q(O,s)的邊長是OA的![]() 倍,
倍,
所以Q(O,s)的邊長不大于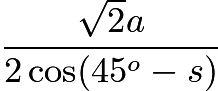 。
。
綜合以上兩種情形的分析,可知Q(O,s)的邊長不大于![]() ,
,
其中,
![]() ,
,
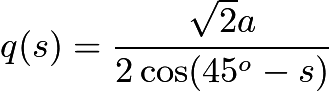 。
。
(1) 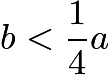 ,即
,即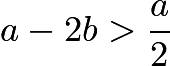 。
。
當![]() 時,
時,![]() 的邊長不大于
的邊長不大于
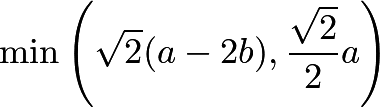
因為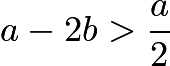 ,所以上式中應取第二項作為最小值。
,所以上式中應取第二項作為最小值。
當s逐步減小時,因為余弦函數的值從0度到45度逐漸減小,所以p(s)的值遞減,而q(s)的值遞增。
取s的值使得p(s)=q(s),且記s的這個特殊值為![]() 。我們來證明
。我們來證明![]() 就是面積最大的正方形。
就是面積最大的正方形。
當![]() 時,
時,![]() ,Q(O,s)的邊長應取q(s),所以比
,Q(O,s)的邊長應取q(s),所以比![]() 的邊長
的邊長![]() 小。
小。
當![]() 時,
時,![]() ,Q(O,s)的邊長應取p(s),也比
,Q(O,s)的邊長應取p(s),也比![]() 的邊長
的邊長![]() 小。
小。
最后,我們來計算![]() (也是
(也是![]() )的值。由
)的值。由![]() 推出
推出
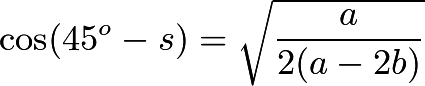
所以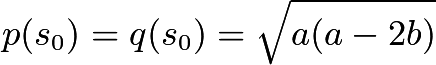 ,因而最大面積為
,因而最大面積為![]() 。
。
在AMC真題中,a=5,b=1,所以最大面積為![]() 。
。
(2) 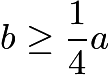 ,即
,即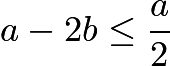 。
。
當![]() 時,
時,![]() 的邊長不大于
的邊長不大于
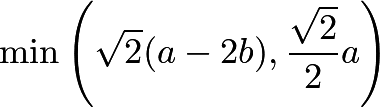
因為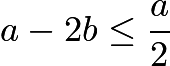 ,所以上式中應取第一項作為最小值。
,所以上式中應取第一項作為最小值。
接下來讓s逐步減小到0度,在這個過程中p(s)的值遞減,而q(s)的值遞增。因此對任意s,p(s)都不大于q(s),所以Q(O,s)的邊長始終取p(s)的值。
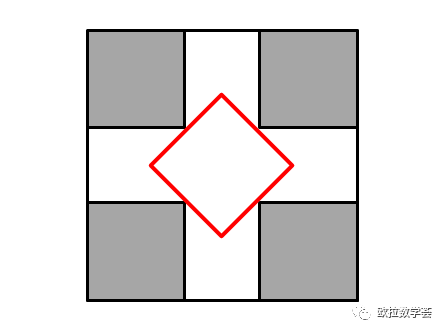
因為p(s)的值在45度時達到最大值![]() ,所以面積最大的Q(0,s),旋轉角度必定是45度,且其面積為
,所以面積最大的Q(0,s),旋轉角度必定是45度,且其面積為![]() 。見下圖。
。見下圖。
總結一下我們上面得到的結論。
當四個角上被切掉的小正方形邊長小于原大正方形的四分之一時(b<a/4),所得的十字形比較“胖”。此時,十字形內可作的正方形的最大面積為a(a-2b),且它與十字形有8個交點。
當四個角上被切掉的小正方形邊長大于等于原大正方形的四分之一時,所得的十字形比較“瘦”。此時,十字形內可作的正方形的面積為![]() ,且其旋轉角都是45度。
,且其旋轉角都是45度。
就推理過程而言,上面的推理省略了一些步驟。在補齊這些步驟后,這就是對問題的一個很完整的數學分析,同時也回答了文章開頭所提的兩個問題。
本文的分析推理過程,也提供了一個簡明的做數學研究的演示范例。如果抱著“做題”的心態,只要根據當前的題目條件找到一個解題路徑,最終得到“正確的答案”,就算是大功告成了。大多數人所理解的“解題能力”,就是這樣的能力。
而數學研究強調的是思考所尋求的答案和題目的條件之間有什么樣的關聯性,講究的是對答案有更全面和深入的了解。并且,還要追問所揭示的關聯性中,有哪些是反映了本質關系的,哪些是特殊情形下的“巧合”。換句話說,就是考慮更一般的情形。
正常的數學教育,以培養解題能力為肇始,進而帶動數學研究能力的提高;從而,數學學習表現優秀的學生,能夠自然地進入數學研究的階段。病態的數學教育,只關注學生在考試中的解題表現,甚至為了更高效地實現這個目標而禁止學生把時間浪費在“與解題無關”的思考上,這實質上是在削弱學生的數學研究能力。
當前盛行的“海量刷題”的數學學習模式,就是病態的數學教育的一種具體形式。一方面,學生們在日趨白熱化的升學競爭中拼盡全力,力求挖盡自己的解題能力;另一方面,他們根本沒有精力提升自己的數學研究能力。結果就是,高分學生的數學研究能力不斷下降。
數學解題能力和研究能力的“剪刀差”現象,是需要非常警惕的問題,其危害性將危及數學教育的根基。

最新發布
? 2025. All Rights Reserved. 滬ICP備2023009024號-1









