- 翰林提供學術活動、國際課程、科研項目一站式留學背景提升服務!
- 400 888 0080
1989 AMC8真題及答案詳解
1989 AMC 8 真題
答案詳細解析請參考文末
Problem 1
![]()
![]()
Problem 2
![]()
![]()
Problem 3
Which of the following numbers is the largest?
![]()
Problem 4
Estimate to determine which of the following numbers is closest to?![]() .
.
![]()
Problem 5
![]()
![]()
Problem 6
If the markings on the number line are equally spaced, what is the number?![]() ?
?
![]()
![]()
Problem 7
If the value of?![]() ?quarters and?
?quarters and?![]() ?dimes equals the value of?
?dimes equals the value of?![]() ?quarters and?
?quarters and?![]() ?dimes, then?
?dimes, then?![]()
![]()
Problem 8
![]()
![]()
Problem 9
There are?![]() ?boys for every?
?boys for every?![]() ?girls in Ms. Johnson's math class. If there are?
?girls in Ms. Johnson's math class. If there are?![]() ?students in her class, what percent of them are boys?
?students in her class, what percent of them are boys?
![]()
Problem 10
What is the number of degrees in the smaller angle between the hour hand and the minute hand on a clock that reads seven o'clock?
![]()
Problem 11
Which of the five "T-like shapes" would be symmetric to the one shown with respect to the dashed line?
![[asy] unitsize(48); for (int a=0; a<3; ++a) { fill((2a+1,1)--(2a+.8,1)--(2a+.8,.8)--(2a+1,.8)--cycle,black); } draw((.8,1)--(0,1)--(0,0)--(1,0)--(1,.8)); draw((2.8,1)--(2,1)--(2,0)--(3,0)--(3,.8)); draw((4.8,1)--(4,1)--(4,0)--(5,0)--(5,.8)); draw((.2,.4)--(.6,.8),linewidth(1)); draw((.4,.6)--(.8,.2),linewidth(1)); draw((2.4,.8)--(2.8,.4),linewidth(1)); draw((2.6,.6)--(2.2,.2),linewidth(1)); draw((4.4,.2)--(4.8,.6),linewidth(1)); draw((4.6,.4)--(4.2,.8),linewidth(1)); draw((7,.2)--(7,1)--(6,1)--(6,0)--(6.8,0)); fill((6.8,0)--(7,0)--(7,.2)--(6.8,.2)--cycle,black); draw((6.2,.6)--(6.6,.2),linewidth(1)); draw((6.4,.4)--(6.8,.8),linewidth(1)); draw((8,.8)--(8,0)--(9,0)--(9,1)--(8.2,1)); fill((8,1)--(8,.8)--(8.2,.8)--(8.2,1)--cycle,black); draw((8.4,.8)--(8.8,.8),linewidth(1)); draw((8.6,.8)--(8.6,.2),linewidth(1)); draw((6,1.2)--(6,1.4)); draw((6,1.6)--(6,1.8)); draw((6,2)--(6,2.2)); draw((6,2.4)--(6,2.6)); draw((6.4,2.2)--(6.4,1.4)--(7.4,1.4)--(7.4,2.4)--(6.6,2.4)); fill((6.4,2.4)--(6.4,2.2)--(6.6,2.2)--(6.6,2.4)--cycle,black); draw((6.6,1.8)--(7,2.2),linewidth(1)); draw((6.8,2)--(7.2,1.6),linewidth(1)); label("(A)",(0,1),W); label("(B)",(2,1),W); label("(C)",(4,1),W); label("(D)",(6,1),W); label("(E)",(8,1),W); [/asy]](https://latex.artofproblemsolving.com/8/5/b/85b5278f5301dd5eedd09368cec2b3df00d135ed.png)
Problem 12
![]()
![]()
Problem 13
![]()
![]()
Problem 14
When placing each of the digits?![]() ?in exactly one of the boxes of this subtraction problem, what is the smallest difference that is possible?
?in exactly one of the boxes of this subtraction problem, what is the smallest difference that is possible?
![]()
![]()
Problem 15
The area of the shaded region?![]() ?in parallelogram?
?in parallelogram?![]() ?is
?is
![[asy] unitsize(10); pair A,B,C,D,E; A=origin; B=(4,8); C=(14,8); D=(10,0); E=(4,0); draw(A--B--C--D--cycle); fill(B--E--D--C--cycle,gray); label("A",A,SW); label("B",B,NW); label("C",C,NE); label("D",D,SE); label("E",E,S); label("$10$",(9,8),N); label("$6$",(7,0),S); label("$8$",(4,4),W); draw((3,0)--(3,1)--(4,1)); [/asy]](https://latex.artofproblemsolving.com/6/0/9/6092322b7c3f4d13fc5df8d5bf92420b2010448d.png)
![]()
Problem 16
In how many ways can?![]() ?be written?as?the sum of two primes?
?be written?as?the sum of two primes?
![]()
Problem 17
The number?![]() ?is between?
?is between?![]() ?and?
?and?![]() . The average of?
. The average of?![]() ,?
,?![]() , and?
, and?![]() ?could be
?could be
![]()
Problem 18
Many calculators have a reciprocal key?![]() ?that replaces the current number displayed with its reciprocal. For example, if the display is?
?that replaces the current number displayed with its reciprocal. For example, if the display is?![]() and the?
and the?![]() ?key is pressed, then the display becomes?
?key is pressed, then the display becomes?![]() . If?
. If?![]() ?is currently displayed, what is the fewest positive number of times you must depress the?
?is currently displayed, what is the fewest positive number of times you must depress the?![]() ?key so the display again reads?
?key so the display again reads?![]() ?
?
![]()
Problem 19
The graph below shows the total accumulated dollars (in millions) spent by the Surf City government during?![]() . For example, about?
. For example, about?![]() ?million had been spent by the beginning of February and approximately?
?million had been spent by the beginning of February and approximately?![]() ?million by the end of April. Approximately how many millions of dollars were spent during the summer months of June, July, and August?
?million by the end of April. Approximately how many millions of dollars were spent during the summer months of June, July, and August?
![]()
![[asy] unitsize(18); for (int a=1; a<13; ++a) { draw((a,0)--(a,.5)); } for (int b=1; b<6; ++b) { draw((-.5,2b)--(0,2b)); } draw((0,0)--(0,12)); draw((0,0)--(14,0)); draw((0,0)--(1,.9)--(2,1.9)--(3,2.6)--(4,4.3)--(5,4.5)--(6,5.7)--(7,8.2)--(8,9.4)--(9,9.8)--(10,10.1)--(11,10.2)--(12,10.5)); label("J",(.5,0),S); label("F",(1.5,0),S); label("M",(2.5,0),S); label("A",(3.5,0),S); label("M",(4.5,0),S); label("J",(5.5,0),S); label("J",(6.5,0),S); label("A",(7.5,0),S); label("S",(8.5,0),S); label("O",(9.5,0),S); label("N",(10.5,0),S); label("D",(11.5,0),S); label("month F=February",(16,0),S); label("$1$",(-.6,2),W); label("$2$",(-.6,4),W); label("$3$",(-.6,6),W); label("$4$",(-.6,8),W); label("$5$",(-.6,10),W); label("dollars in millions",(0,11.9),N); [/asy]](https://latex.artofproblemsolving.com/f/9/c/f9cddde1c49e870e60dd9a1051526987030e4fb6.png)
Problem 20
The figure may be folded along the lines shown to form a number cube. Three number faces come together at each corner of the cube. What is the largest sum of three numbers whose faces come together at a corner?
![[asy] draw((0,0)--(0,1)--(1,1)--(1,2)--(2,2)--(2,1)--(4,1)--(4,0)--(2,0)--(2,-1)--(1,-1)--(1,0)--cycle); draw((1,0)--(1,1)--(2,1)--(2,0)--cycle); draw((3,1)--(3,0)); label("$1$",(1.5,1.25),N); label("$2$",(1.5,.25),N); label("$3$",(1.5,-.75),N); label("$4$",(2.5,.25),N); label("$5$",(3.5,.25),N); label("$6$",(.5,.25),N); [/asy]](https://latex.artofproblemsolving.com/a/9/d/a9d2852b04663db7cd9afc83d7f7065db8ceb539.png)
![]()
Problem 21
Jack had a bag of?![]() ?apples. He sold?
?apples. He sold?![]() ?of them to Jill. Next he sold?
?of them to Jill. Next he sold?![]() ?of those remaining to June. Of those apples still in his bag, he gave the shiniest one to his teacher. How many apples did Jack have then?
?of those remaining to June. Of those apples still in his bag, he gave the shiniest one to his teacher. How many apples did Jack have then?
![]()
Problem 22
The letters?![]() ,?
,?![]() ,?
,?![]() ,?
,?![]() ,?
,?![]() ,?
,?![]() ?and the digits?
?and the digits?![]() ,?
,?![]() ,?
,?![]() ,?
,?![]() ?are "cycled" separately?as?follows and put together in a numbered list:
?are "cycled" separately?as?follows and put together in a numbered list:![[begin{tabular}[t]{lccc} & & AJHSME & 1989 \ & & & \ 1. & & JHSMEA & 9891 \ 2. & & HSMEAJ & 8919 \ 3. & & SMEAJH & 9198 \ & & ........ & end{tabular}]](https://latex.artofproblemsolving.com/7/1/1/7118a46dde66777eaf400e8ea2209dc386da0af5.png)
What is the number of the line on which?![]() ?will appear for the first time?
?will appear for the first time?
![]()
Problem 23
An artist has?![]() ?cubes, each with an edge of?
?cubes, each with an edge of?![]() ?meter. She stands them on the ground to form a sculpture?as?shown. She then paints the exposed surface of the sculpture. How many square meters does she paint?
?meter. She stands them on the ground to form a sculpture?as?shown. She then paints the exposed surface of the sculpture. How many square meters does she paint?
![]()
![[asy] draw((0,0)--(2.35,-.15)--(2.44,.81)--(.09,.96)--cycle); draw((.783333333,-.05)--(.873333333,.91)--(1.135,1.135)); draw((1.566666667,-.1)--(1.656666667,.86)--(1.89,1.1)); draw((2.35,-.15)--(4.3,1.5)--(4.39,2.46)--(2.44,.81)); draw((3,.4)--(3.09,1.36)--(2.61,1.4)); draw((3.65,.95)--(3.74,1.91)--(3.29,1.94)); draw((.09,.96)--(.76,1.49)--(.71,1.17)--(2.2,1.1)--(3.6,2.2)--(3.62,2.52)--(4.39,2.46)); draw((.76,1.49)--(.82,1.96)--(2.28,1.89)--(2.2,1.1)); draw((2.28,1.89)--(3.68,2.99)--(3.62,2.52)); draw((1.455,1.135)--(1.55,1.925)--(1.89,2.26)); draw((2.5,2.48)--(2.98,2.44)--(2.9,1.65)); draw((.82,1.96)--(1.55,2.6)--(1.51,2.3)--(2.2,2.26)--(2.9,2.8)--(2.93,3.05)--(3.68,2.99)); draw((1.55,2.6)--(1.59,3.09)--(2.28,3.05)--(2.2,2.26)); draw((2.28,3.05)--(2.98,3.59)--(2.93,3.05)); draw((1.59,3.09)--(2.29,3.63)--(2.98,3.59)); [/asy]](https://latex.artofproblemsolving.com/c/9/0/c907b9d8e0a7e2f4eb5dc0d61c0fe69439512738.png)
Problem 24
Suppose a square piece of paper is folded in half vertically. The folded paper is then cut in half along the dashed line. Three rectangles are formed-a large one and two small ones. What is the ratio of the perimeter of one of the small rectangles to the perimeter of the large rectangle?
![]()
![[asy] draw((0,0)--(0,8)--(6,8)--(6,0)--cycle); draw((0,8)--(5,9)--(5,8)); draw((3,-1.5)--(3,10.3),dashed); draw((0,5.5)..(-.75,4.75)..(0,4)); draw((0,4)--(1.5,4),EndArrow); [/asy]](https://latex.artofproblemsolving.com/6/a/b/6ab13c6ad222a415ca8ff4bfb6135d981e1c657c.png)
Problem 25
Every time these two wheels are spun, two numbers are selected by the pointers. What is the probability that the sum of the two selected numbers is even?
![]()
![[asy] unitsize(36); draw(circle((-3,0),1)); draw(circle((0,0),1)); draw((0,0)--dir(30)); draw((0,0)--(0,-1)); draw((0,0)--dir(150)); draw((-2.293,.707)--(-3.707,-.707)); draw((-2.293,-.707)--(-3.707,.707)); fill((-2.9,1)--(-2.65,1.25)--(-2.65,1.6)--(-3.35,1.6)--(-3.35,1.25)--(-3.1,1)--cycle,black); fill((.1,1)--(.35,1.25)--(.35,1.6)--(-.35,1.6)--(-.35,1.25)--(-.1,1)--cycle,black); label("$5$",(-3,.2),N); label("$3$",(-3.2,0),W); label("$4$",(-3,-.2),S); label("$8$",(-2.8,0),E); label("$6$",(0,.2),N); label("$9$",(-.2,.1),SW); label("$7$",(.2,.1),SE); [/asy]](https://latex.artofproblemsolving.com/1/7/c/17ccafee32c561156cef7b2bced57d414ca76485.png)
1989 AMC8真答案詳細解析
1.We make use of the associative?and?commutative?properties of?addition?to rearrange the?sum?as![]()
2.
3.We have?![]() , so choice?
, so choice?![]() ?is the largest.
?is the largest.
4.![]() ?is around?
?is around?![]() ?and?
?and?![]() ?is around?
?is around?![]() ?so the?fraction?is approximately
?so the?fraction?is approximately![]()
5.We use the?order of operations?here to get

6.Five steps are taken to get from?![]() ?to?
?to?![]() . Each step is of equal size, so each step is?
. Each step is of equal size, so each step is?![]() . Three steps are taken from?
. Three steps are taken from?![]() ?to?
?to?![]() , so?
, so?![]() .
.
7.
8.
Solution 1
We use the distributive property to get![]()
Solution 2
Since?![]() , we have
, we have![]() The only answer choice greater than?
The only answer choice greater than?![]() ?is?
?is?![]() .
.
9.Besides ensuring the situation is possible, the?![]() ?students information is irrelevant.
?students information is irrelevant.
From the first statement, we can deduce that?![]() ?of every?
?of every?![]() ?students are boys. Thus,?
?students are boys. Thus,?![]() ?of the students are boys.
?of the students are boys.
10.The smaller angle makes up?![]() ?of the?circle?which is the clock. A circle is?
?of the?circle?which is the clock. A circle is?![]() , so the measure of the smaller angle is
, so the measure of the smaller angle is![]()
11.Drawing the?reflection, we see that it is?![]() . Imagine it?as?if it were a mirror reflection or if you were to flip it over the dashed line.
. Imagine it?as?if it were a mirror reflection or if you were to flip it over the dashed line.
12.
13.
14.When trying to?minimize![]() , we minimize?
, we minimize?![]() ?and?maximize
?and?maximize![]() . Since in this problem,?
. Since in this problem,?![]() ?is three digit and?
?is three digit and?![]() ?is two digit, we set?
?is two digit, we set?![]() ?and?
?and?![]() . Their difference is?
. Their difference is?![]() .
.
15.
Solution 1
Let?![]() ?denote the area of figure?
?denote the area of figure?![]() .
.
Clearly,?![]() . Using basic area formulas,
. Using basic area formulas,
Finally, we have?![]()
Solution 2
Notice that?![]() ?is a trapezoid. Therefore its area is
?is a trapezoid. Therefore its area is![]()
16.For?![]() ?to be written?as?the sum of two?integers, one must be?odd?and the other must be even. There is only one?even?prime, namely?
?to be written?as?the sum of two?integers, one must be?odd?and the other must be even. There is only one?even?prime, namely?![]() , so one of the numbers must be?
, so one of the numbers must be?![]() , making the other?
, making the other?![]() .
.
However,?![]() ?is not prime, so there are no ways to write?
?is not prime, so there are no ways to write?![]() ?as?the sum of two primes?
?as?the sum of two primes?![]() .
.
17.
We know that?![]() ?and we wish to bound?
?and we wish to bound?![]() .
.
From what we know, we can deduce that?![]() , and thus
, and thus![]()
The only answer choice that falls in this range is choice?![]()
18.Let?![]() . We have
. We have![]() Thus, we need to iterate the key pressing twice to get the display back to the original?
Thus, we need to iterate the key pressing twice to get the display back to the original?![]() .
.
19.Since we want to know how much money is spent in June, July and August, we need the?difference?between the amount of money spent by the beginning of June and the amount of money spent by the end of August.
We estimate these to be about?![]() ?million and?
?million and?![]() ?million, respectively. The difference is
?million, respectively. The difference is![]()
20.It is clear that?![]() ,?
,?![]() , and?
, and?![]() ?will not come together to get a?sum?of?
?will not come together to get a?sum?of?![]() .
.
The faces?![]() ,?
,?![]() , and?
, and?![]() ?come together at a common vertex, making the?maximal?sum?
?come together at a common vertex, making the?maximal?sum?![]() .
.
21.First he gives?![]() ?apples to Jill, so he has?
?apples to Jill, so he has?![]() ?apples left. Then he gives?
?apples left. Then he gives?![]() ?apples to June, so he has?
?apples to June, so he has?![]() ?left.
?left.
Finally, he gives one to the teacher, leaving?![]()
22.Every?![]() ?line has?
?line has?![]() ?as?part of it and every?
?as?part of it and every?![]() ?line has?
?line has?![]() ?as?part of it. In order for both to be part of line?
?as?part of it. In order for both to be part of line?![]() ,?
,?![]() ?must be a multiple of?
?must be a multiple of?![]() ?and?
?and?![]() , the least of which is?
, the least of which is?![]() .
.
23.
We can consider the contributions of the sides of the three layers and the tops of the layers separately.
Layer?![]() ?(counting from the top starting at?
?(counting from the top starting at?![]() ) has?
) has?![]() ?side faces each with?
?side faces each with?![]() ?unit squares, so the sides of the pyramid contribute?
?unit squares, so the sides of the pyramid contribute?![]() for the surface area.
for the surface area.
The tops of the layers when combined form the same arrangement of unit cubes?as?the bottom of the pyramid, which is a?![]() ?square, hence this contributes?
?square, hence this contributes?![]() ?for the surface area.
?for the surface area.
Thus, the artist paints?![]() ?square meters.
?square meters.
24.
From here on a blue line represents a cut, the dashed line represents the fold.
![[asy] draw((0,0)--(4,0)--(4,4)--(0,4)--cycle,linewidth(1)); draw((1,0)--(1,4),blue+linewidth(1)); draw((2,0)--(2,4),dashed); draw((3,0)--(3,4),blue+linewidth(1)); label("$x$",(0.5,4),N); label("$x$",(1.5,4),N); label("$x$",(2.5,4),N); label("$x$",(3.5,4),N); label("$4x$",(0,2),W); [/asy]](https://latex.artofproblemsolving.com/8/7/e/87eaf90020921c5f0b0a692a128d18a6aad5a735.png)
From the diagram, we can tell the?perimeter?of one of the small rectangles is?![]() ?and the perimeter of the large?rectangle?is?
?and the perimeter of the large?rectangle?is?![]() . The desired?ratio?is
. The desired?ratio?is![]()
25.
For the?sum?to be?even, the two selected numbers must have the same?parity.
The first spinner has?![]() ?odd numbers and?
?odd numbers and?![]() ?even, so no matter what the second spinner is, there is a?
?even, so no matter what the second spinner is, there is a?![]() ?chance the first spinner lands on a number with the same parity, so the?probability?of an even sum is?
?chance the first spinner lands on a number with the same parity, so the?probability?of an even sum is?![]() .
.
以上解析方式僅供參考
學術活動報名掃碼了解!免費領取歷年真題!
翰林AMC8課程體系流程圖
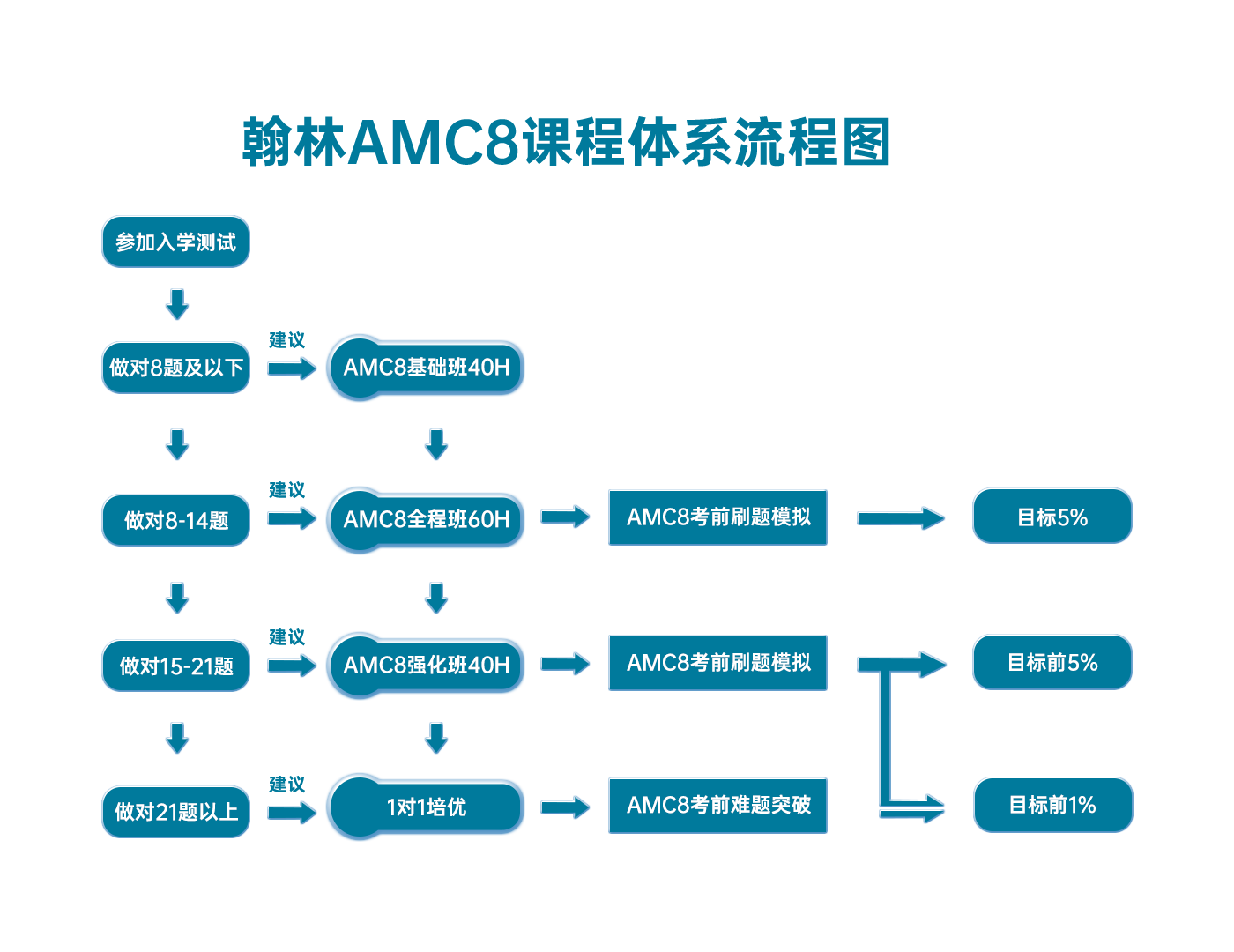

最新發布
? 2025. All Rights Reserved. 滬ICP備2023009024號-1









