AMC10/12 A卷完美收官!
?最新考試真題速來看!
翰林國際教育在得到試題的第一時間
就快馬加鞭為同學(xué)們整理好了!
一起來看看此次新鮮出爐的真題吧!
翰林在官方允許試題解禁的第一時間
為大家宣布真題,答案及解析!
01AMC10 A卷考試真題
1.What is the value of (22?2)-(32?3)+(42?4)?
(A) 1? (B) 2? (C) 5? (D) 8? (E) 12
2.?Portia’s high school has 3 times as many students as Lara’s high school. The two high ?schools have a total of 2600 students. How many students does Portia’s high school ?have?
(A) 600? (B) 650? (C) 1950? (D) 2000? (E) 2050
3.The sum of two natural numbers is 17,402. One of the two numbers is divisible by ?10. If the units digit of that number is erased, the other number is obtained. What is the ?difference of these two numbers?
(A) 10,272? (B) 11,700? (C) 13,362? (D) 14,238? (E) 15,426
4.A cart rolls down a hill, traveling 5 inches the first second and accelerating so that ?during each successive 1-second time interval, it travels 7 inches more than during the ?previous 1-second interval. The cart takes 30 seconds to reach the bottom of the hill. ?How far, in inches, does it travel?
(A) 215? (B) 360? (C) 2992? (D) 3195? (E) 3242
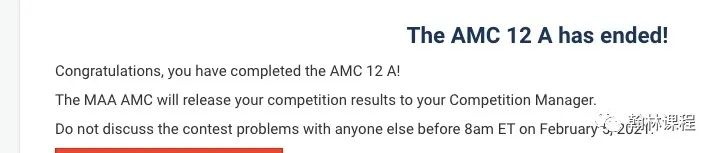
5.The quiz scores of a class with k>12 students have a mean of 8. The mean of a ?collection of 12 of these quiz scores is 14. What is the mean of the remaining quiz ?scores in terms of k?
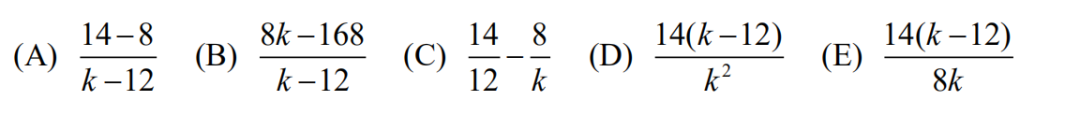
6.Chantal and Jean start hiking from a trailhead toward a fire tower. Jean is wearing a ?heavy backpack and walks slower. Chantal starts walking at 4 miles per hour. Halfway ?to the tower, the trail becomes really steep, and Chantal slows down to 2 miles per hour. ?After reaching the tower, she immediately turns around and descends the steep part of ?the trail at 3 miles per hour. She meets Jean at the halfway point. What was Jean’s ?average speed, in miles per hour, until they meet?
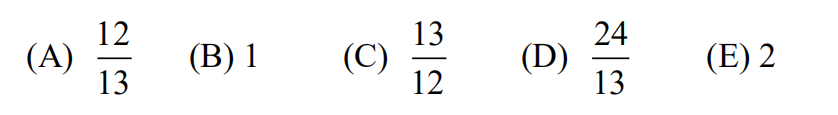
7.?Tom has a collection of 13 snakes, 4 of which are purple and 5 of which are happy. ?He observes that
? all of his happy snakes can add
? none of his purple snakes can subtract, and
? all of his snakes that can’t subtract also can’t add.
Which of these conclusions can be drawn about Tom’s snakes?
(A) Purple snakes can add.
(B) Purple snakes are happy.
(C) Snakes that can add are purple.
(D) Happy snakes are not purple.
(E) Happy snakes can’t subtract.
8.When a student multiplied the number 66 by the repeating decimal,
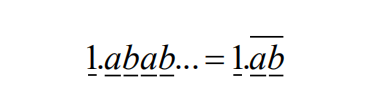 Where a and b are digits, he did not notice the notation and just multiplied 66 times
Where a and b are digits, he did not notice the notation and just multiplied 66 times
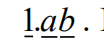 ?Later he found that his answer is 0.5 less than the correct answer. What is the 2- digit integer?ab??
?Later he found that his answer is 0.5 less than the correct answer. What is the 2- digit integer?ab??
(A) 15? (B) 30? (C) 45? (D) 60? (E) 75
9.What is the least possible value of
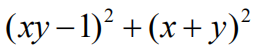 for real numbers x and y?
for real numbers x and y?
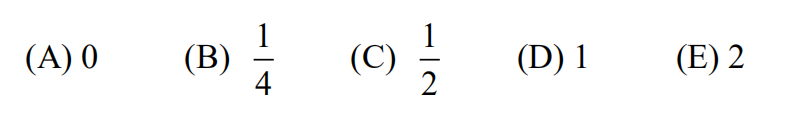 10.Which of the following is equivalent to
10.Which of the following is equivalent to
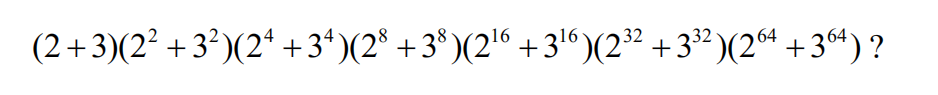
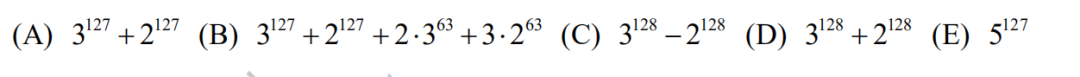 11.For which of the following integers b is the base-b number 2021b?221b not divisible ?by 3?
11.For which of the following integers b is the base-b number 2021b?221b not divisible ?by 3?
(A) 3? (B) 4? (C) 6? (D) 7? (E) 8
12.Two right circular cones with vertices facing down as shown in the figure below ?contain the same amount of liquid. The radii of the top of the liquid surfaces are 3cm ?and 6cm. Into each cone is dropped a spherical marble of radius 1cm, which sinks to ?the bottom and is completely submerged without spilling any liquid. What is the ratio ?of the rise of the liquid level in the narrow cone to the liquid level in the wide cone?
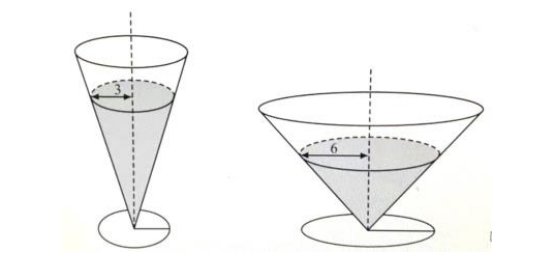
(A) 1:1? (B) 47:43? (C) 2:1? (D) 40:13? (E) 4:1
13.What is the volume of tetrahedron ABCD with edge lengths AB=2, AC=3, AD=4
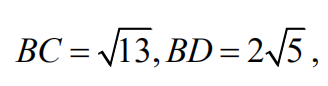 and CD=5?
and CD=5?
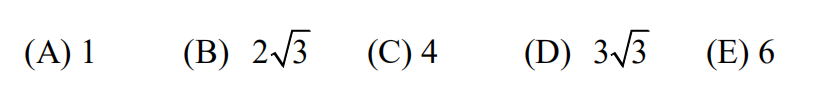 14.Ali the roots of polynomial
14.Ali the roots of polynomial
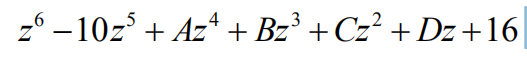 are positive ?integers, possibly repeated. What is the value of B?
are positive ?integers, possibly repeated. What is the value of B?
(A) -88? (B) -80? (C) -64? (D) -41? (E) -40
15.Values for A, B, C, and D are to be selected from {1, 2, 3, 4, 5, 6} without ?replacement (i.e., no two letters have the same value). How many ways are there to ?make such choices so that the two curves y = Ax2+B and y = Cx2+D intersect? (The order in which the curves are listed does not matter; for example, the choices A=3. ?B=2, C=4, D=1 is considered the same as the choices A = 4, B=1, C= 3. D=2.)
 16.In the following list of numbers, the integer n appears n times in the list for 1≤n ≤200
16.In the following list of numbers, the integer n appears n times in the list for 1≤n ≤200
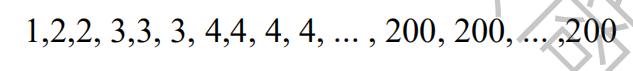 What is the median of the numbers in this list?
What is the median of the numbers in this list?
(A) 100.5? (B) 134? (C) 142? (D) 150.5? (E) 167
17.

(A) 65? (B) 132? (C) 157? (D) 194? (E) 215
18.

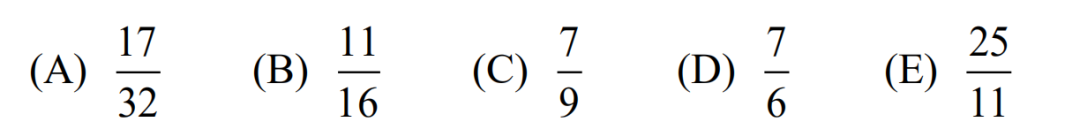 19.The area of the region bounded by the graph of
19.The area of the region bounded by the graph of
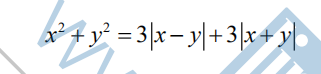 is m+nπ, where m and n are integers. What is m+n?
is m+nπ, where m and n are integers. What is m+n?
(A) 18? (B) 27? (C) 36? (D) 45? (E) 54
20.In how many ways can the sequence 1,2,3,4,5 be rearranged so that no three ?consecutive terms are increasing and no three consecutive terms are decreasing?
(A) 10? (B) 18? (C) 24? (D) 32? (E) 44
21.

(A) 47? (B) 52? (C) 55? (D) 58? (E) 63
22.Hiram's algebra notes are 50 pages long and are printed on 25 sheets of paper: the ?first sheet contains pages 1 and 2 the second sheet contains pages 3 and 4. and so on. ?One day he leaves his notes on the table before leaving for lunch. and his roommate decides to borrow some pages from the middle of the notes. When Hiram comes back, ?he discovers that his roommate has taken a consecutive set of sheets from the notes and ?that the average (mean) of the page numbers on all remaining sheets is exactly 19 How ?many sheets were borrowed?
(A) 10? (B) 13? (C) 15? (D) 17? (E) 20
23.Frieda the frog begins a sequence of hops on a 3×3 grid of squares, moving one ?square on each hop and choosing at random the direction of each hop up, down, left, or ?right. She does not hop diagonally. When the direction of a hop would take Frieda off the grid, she "wraps around" and jumps to the opposite edge. For example If Frieda ?begins in the center square and makes two hops "up”, the first hop would place her In ?the top row middle square, and the second hop would cause Frieda to Jump to the opposite edge, landing in the bottom row middle square. Suppose Frieda starts from the ?center square, makes at most four hops at random, and stops hopping If she lands on a ?comer square. What Is the probability that she reaches a corner square on one of the ?four hops?
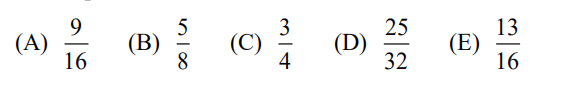 24.
24.

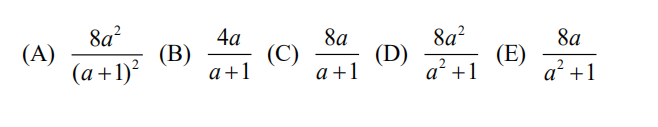 25.How many ways are there to place 3 Indistinguishable red chips, 3 indistinguishable ?blue chips, and 3 Indistinguishable green chips in the squares of a 3×3 grid so that no ?two chips of the same color are directly adjacent 10 each other, either vertically or horizontally?
25.How many ways are there to place 3 Indistinguishable red chips, 3 indistinguishable ?blue chips, and 3 Indistinguishable green chips in the squares of a 3×3 grid so that no ?two chips of the same color are directly adjacent 10 each other, either vertically or horizontally?
(A) 12? (B) 18? (C) 24? (D) 30? (E) 36
02AMC12 A卷考試真題
1.What is the value of
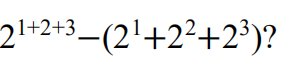
(A) 0? (B) 50? (C) 52? (D) 54? (E) 57
2.Under what conditions is
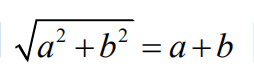 true, where a and b are real numbers?
true, where a and b are real numbers?
(A) It is never true
(B) It is true if and only if ab=0
(C) It is true if and only if a+b≥0
(D) It is true if and only if ab=0 and a+b≥0
(E) It is always true
3.The sum of two natural numbers is 17,402. One of the two numbers is divisible by ?10. If the units digit of that number is erased, the other number is obtained. What is the ?difference of these two numbers?
(A) 10,272(B) 11,700?(C) 13,,362??(D) 14,238??(E) 15,426
4.Tom has a collection of 13 snakes, 4 of which are purple and 5 of which are happy. ?He observes that
? all of his happy snakes can add
? none of his purple snakes can subtract, and
? all of his snakes that can’t subtract also can’t add
Which of these conclusions can be drawn about Tom’s snakes?
(A) Purple snakes can add.
(B) Purple snakes are happy.
(C) Snakes that can add are purple.
(D) Happy snakes are not purple.
(E) Happy snakes can’t subtract.
5.When a student multiplied the number 66 by the repeating decimal,
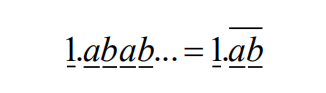 Where a and b are digits, he did not notice the notation and just multiplied 66 times?1.ab?. Later he found that his answer is 0.5 less than the correct answer. What is the 2- digit integer?ab??
Where a and b are digits, he did not notice the notation and just multiplied 66 times?1.ab?. Later he found that his answer is 0.5 less than the correct answer. What is the 2- digit integer?ab??
(A) 15? (B) 30? (C) 45? (D) 60? (E) 75
6.A deck of cards has only red cards and black cards. The probability of a randomly ?chosen card being red is? 1/3. When 4 black cards are added to the deck, the probability ?of choosing red becomes 1/4?. How many cards were in the deck originally?
(A) 6? (B) 9? (C) 12? (D) 15? (E) 18
7.What is the least possible value of
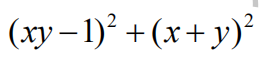 for real numbers x and y?
for real numbers x and y?
 8.A sequence of numbers is defined by D0 = 0, D1 = 0, D2 =1 and Dn= Dn-1 + Dn-3 for ?n≥3. What are the parities (evenness or oddness) of the triple of numbers (D2021, D2022, ?D2013), where E denotes even and 0 denotes odd
8.A sequence of numbers is defined by D0 = 0, D1 = 0, D2 =1 and Dn= Dn-1 + Dn-3 for ?n≥3. What are the parities (evenness or oddness) of the triple of numbers (D2021, D2022, ?D2013), where E denotes even and 0 denotes odd
(A) (O, E, O)
(B) (E, E, O)
(C) (E, O, E)
(D) (O, O, E)
(E) (O, O, O)
9.Which of the following is equivalent to
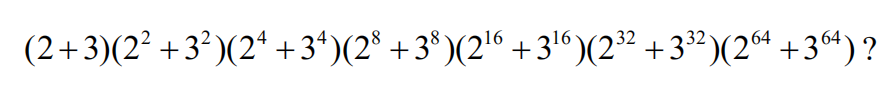
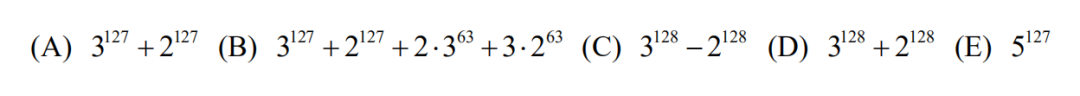 10.Two right circular cones with vertices facing down as shown in the figure below ?contain the same amount of liquid. The radii of the top of the liquid surfaces are 3cm ?and 6cm. Into each cone is dropped a spherical marble of radius 1cm, which sinks to ?the bottom and is completely submerged without spilling any liquid. What is the ratio ?of the rise of the liquid level in the narrow cone to the liquid level in the wide cone?
10.Two right circular cones with vertices facing down as shown in the figure below ?contain the same amount of liquid. The radii of the top of the liquid surfaces are 3cm ?and 6cm. Into each cone is dropped a spherical marble of radius 1cm, which sinks to ?the bottom and is completely submerged without spilling any liquid. What is the ratio ?of the rise of the liquid level in the narrow cone to the liquid level in the wide cone?
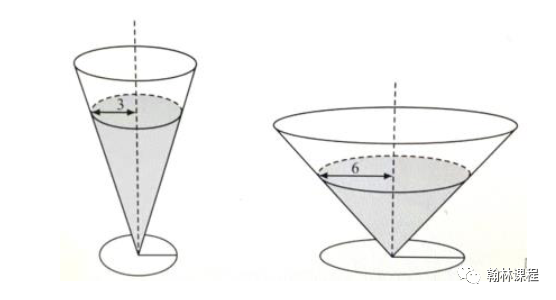
(A) 1:1? (B) 47:43? (C) 2:1? (D) 40:13? (E) 4:1
11.A laser is placed at the point (3, 5). The laser beam travels in a straight line. Larry ?wants the beam to hit and bounce off the y-axis, then hit and bounce off the x-axis, the ?hit the point (7, 5). What is the total distance the beam will travel along this path?
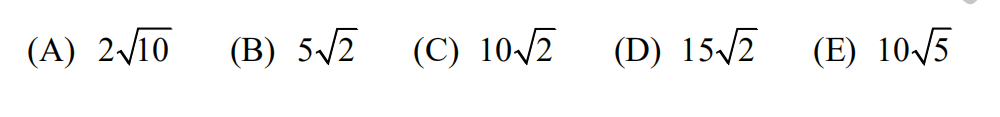 12.Ali the roots of polynomial are positive
12.Ali the roots of polynomial are positive
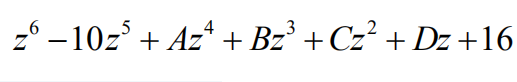 integers, possibly repeated. What is the value of B?
integers, possibly repeated. What is the value of B?
(A) -88? (B) -80? (C) -64? (D) -41? (E) -40
13.Of the following complex number z, which one has the property that z5 has the ?greatest real part?
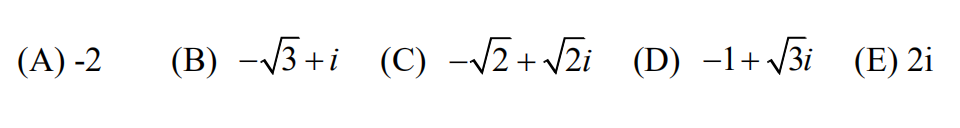 14.
14.
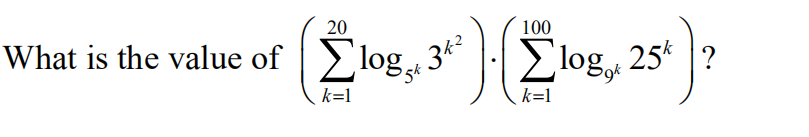
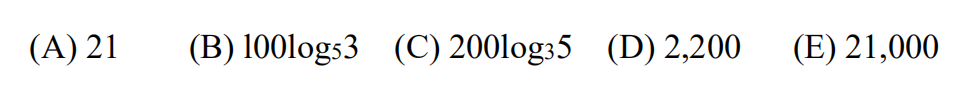
15.A choir director must select a group of singers from among his 6 tenors and 8 basses. ?The only requirements are that the difference between the numbers of tenors and basses ?must be a multiple of 4, and the group must have at least one singer. Let N be the number ?of groups that could be selected. What is the remainder when N is divided by 100?
(A) 47? (B) 48? (C) 83? (D) 95? (E) 9616.In the following list of numbers, the integer n appears n times in the list for 1≤n ≤200
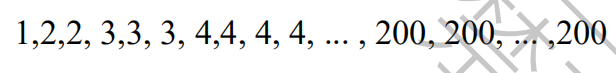 What is the median of the numbers in this list?
What is the median of the numbers in this list?
(A) 100.5? (B) 134? (C) 142? (D) 150.5? (E) 167
17.

(A) 65? (B) 132? (C) 157? (D) 194? (E) 215
18.

 19.How many solutions does the equation sin
19.How many solutions does the equation sin
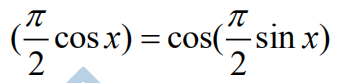 have in the ?closed interval [0,π ]
have in the ?closed interval [0,π ]
(A) 0? (B) 1? (C) 2? (D) 3? (E) 4
20.Suppose that on a parabola with vertex V and focus F there exists a point A such ?that AF=20 and AV=21. What is the sum of all possible values of the length FV?
 21.
21.

(A) 7? (B) 9? (C) 11? (D) 13? (E) 15
22.

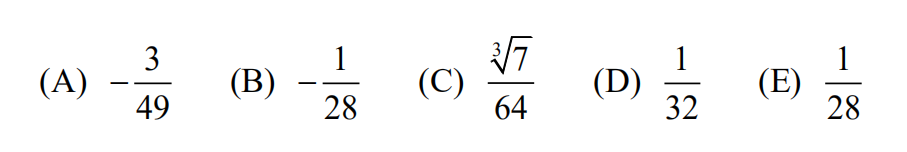
23.Frieda the frog begins a sequence of hops on a 3×3 grid of squares, moving one ?square on each hop and choosing at random the direction of each hop up, down, left, or ?right. She does not hop diagonally. When the direction of a hop would take Frieda off the grid, she "wraps around" and jumps to the opposite edge. For example If Frieda ?begins in the center square and makes two hops "up”, the first hop would place her In ?the top row middle square, and the second hop would cause Frieda to Jump to the opposite edge, landing in the bottom row middle square. Suppose Frieda starts from the ?center square, makes at most four hops at random, and stops hopping If she lands on a ?comer square. What Is the probability that she reaches a corner square on one of the ?four hops?
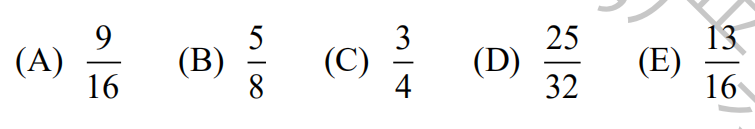 24.
24.

(A) 110? (B) 114? (C) 118? (D) 122? (E) 126
25.Let d(n) denote the number of positive integers that divide n, including 1 and n. For ?example, d(1)=1, d(2)=2, and d(12)=6. (This function is known as the divisor function.) ?Let
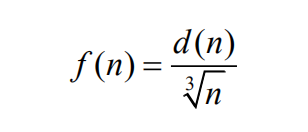
There?is?a?unique?positive?integer?N?such?that?f(N)>f(n)?for?all?positive?integers?n≠N.?what?is?the?sum?of?the?digits?of?N?
(A) 5? (B) 6? (C) 7? (D) 8? (E) 9
以上就是剛剛結(jié)束的AMC10/12 A卷的全部真題了
小伙伴們都考的如何呢?
AMC10/12 B卷將2月11日準(zhǔn)時開考
預(yù)祝各位考生旗開得勝,斬獲佳績!
想要獲取AMC10/12 A卷真題的答案嗎?
想要提前聽名師的真題講解視頻嗎?
掃描下方二維碼,獲取真題答案哦!
03 備戰(zhàn)AMC,從現(xiàn)在開始!
AMC系列考試最具有含金量的爬藤學(xué)術(shù)活動!想要先人一步在AMC考試中考出好成績嗎?翰林金牌AMC課程助力你的大考!
數(shù)學(xué)學(xué)術(shù)活動類班課
| 班課名稱 | 人數(shù) | 班課時間 |
| AMC8基礎(chǔ)班 | 3-8人 | 5.8~9.18? ?09:00~11:00 |
| AMC10刷題班 | 3-8人 | 2.6 上午10-12下午4-6
2.7下午1-3 2.8-2.10上午10-12下午4-6 |
| AMC10基礎(chǔ)全程班 | 3-8人 | 3.6-7.3 ?每周六10:00-12:00 ?7.10-8.28 每周六9-12 |
| AMC10基礎(chǔ)全程班 | 3-8人 | 3.6-7.17?每周六19:00-21:00 |
| AMC10基礎(chǔ)全程班 | 3-8人 | 3.7-7.4 每周日10:00-12:00 ?7.11-8.29 每周日9:00-12:00 |
| AMC10基礎(chǔ)全程班 | 3-8人 | 3.7-7.18?每周日14:00-17:00 |
| AMC10基礎(chǔ)全程班 | 3-8人 | 3.7-7.18每周日上午8-11 |
| AMC10強(qiáng)化班 | 3-8人 | 4.18-8.29每周日9:00-11:00 |
| AMC10強(qiáng)化班 | 3-8人 | 4.11-8.22每周日19:00-21:00 |
| AMC12刷題班 | 3-8人 | 2.6-2.10 ?每天上午10-12?及 下午2:00-4 :00 |
| AMC12基礎(chǔ)全程班 | 3-8人 | 2.21-9.12
每周日下午2:00~4:00 |
| AMC12基礎(chǔ)全程班 | 3-8人 | 3.7-7.4 每周日10:00-12:00 ?7.11-8.29 每周日9-12 |
| AMC12基礎(chǔ)全程班 | 3-8人 | 3.6-8.21?每周六19:00-22:00 |
| AMC12基礎(chǔ)全程班 | 3-8人 | 3.6-7.3 ?每周六10:00-12:00 ?7.10-8.28 每周六9-12 |
| AMC12基礎(chǔ)全程班 | 3-8人 | 3.13-7.10 ?每周六10:00-12:00 ?7.17-9.4 每周六9-12 |
| AMC12基礎(chǔ)班 | 3-8人 | 4.10-8.21每周六19:00-22:00 |
| AMC12強(qiáng)化班 | 3-8人 | 3.13-7.17每周六14:00-16:00 |
| AMC12強(qiáng)化班 | 3-8人 | 4.10-8.21每周六19:00-21:00 |
| AMC12強(qiáng)化班 | 3-8人 | 4.11-8.22每周日14:00-16:00 |
| AMC12強(qiáng)化班 | 3-8人 | 4.10-8.21每周日19:00-21:00 |
| BmMT全程班 | 3-8人 | 1.9-3.6 每周六日13:00-15:00 ?(2.12,2.13休息) |
| BmMT全程班 | 3-8人 | 1.9-3.6 每周六日8:00-10:00 ? (2.12,2.13休息)
(最后一次課需要調(diào)整待定) |
| Mathleague第二階段
(3-4年級) |
3-8人 | 2/1-2/19每周一到周五
上午9-11(2/10-2/16休息) |
| Mathleague第二階段
(5-6年級) |
3-8人 | 2/1-2/19 每周一到周五下午2-4(2/10-2/16休息) |
| Mathleague第二階段
(7-8年級) |
3-8人 | 2/1-2/19 每周一到周五晚上6-8(2/10-2/16休息) |
| 袋鼠3-4年級班 | 3-8人 | 1.16-3.21 每周六周日
14:00-16:00 |
| 袋鼠5-6年級班 | 3-8人 | 1.16-3.27 每周六周日16:30-18:30(1.17休息) |
數(shù)學(xué)學(xué)術(shù)活動戰(zhàn)績(2017-2020)
美國AMC系列
🏆2020翰林學(xué)員美國考團(tuán)AIME晉級率93.3%,目前已統(tǒng)計(jì)到的參考學(xué)員AIME晉級率90.9%。來自全國各地的10位學(xué)員在AMC12B卷中獲得了平均123分的好成績,均分超過DHR!所有AMC12A+B聯(lián)考學(xué)員均獲得大幅度提分,平均提分39.75分。
🏆2019-2020賽季,AMC12B最高分132分,AMC12A最高分118.3分,AMC10B最高分133.5分,兩位學(xué)員AIME分別以11分與12分晉級USAMO美國數(shù)學(xué)奧林匹克。
🏆2019翰林學(xué)員中1名AMC8滿分,根據(jù)已有反饋:AMC10A美高學(xué)員均分123分,AMC10B學(xué)員均分124分,AMC12A美高學(xué)員均分108分,AMC10B學(xué)員均分111分;除部分未參賽學(xué)員,AMC10/12小班課學(xué)員綜合AIME晉級率52/67,接近80%。
🏆2018翰林學(xué)員中2名AMC8滿分,AMC10均分126,AMC12均分115,一對一學(xué)員AIME晉級率100%,AIME最高分12/15。
澳洲AMC
🏆2020澳洲AMC翰林學(xué)員中 A等級:一等獎2名,二等獎2名,三等獎2名。B等級:二等獎1名,三等獎2名。D等級:一等獎1名,二等獎1名。E等級:二等獎1名。
Euclid歐幾里得數(shù)學(xué)學(xué)術(shù)活動
🏆2019歐幾里得數(shù)學(xué)學(xué)術(shù)活動翰林學(xué)員,75-80分2人, 84-87分5人。
ARML系列
🏆2020ARML區(qū)域賽個人賽:1人華西賽區(qū)前20,1人華南賽區(qū)前100。
🏆2020ARML區(qū)域賽團(tuán)隊(duì)賽:5位學(xué)員獲得團(tuán)隊(duì)銅獎,并晉級下一輪晉級挑戰(zhàn)賽(power contest)(團(tuán)隊(duì)編號604)。
Math League數(shù)學(xué)大聯(lián)盟
🏆2019Math League學(xué)術(shù)活動第一階段:翰林學(xué)員一等獎12名,二等獎18名,三等獎13名,獲獎率95%(參賽學(xué)生45位,43位獲獎);第二階段:18名學(xué)生全部晉級美國總決賽,晉級率100%。
🏆2020夏季挑戰(zhàn)賽,翰林學(xué)員獲得金獎6枚,銀獎6枚,銅獎7枚,4名學(xué)員獲得優(yōu)勝獎。
BMT伯克利數(shù)學(xué)思維挑戰(zhàn)
🏆2020BMT翰林學(xué)員在個人特長賽微積分比賽中獲得全球唯一滿分,個人特長賽代數(shù)比賽獲得中國區(qū)前三,中國區(qū)團(tuán)隊(duì)二等獎,1名學(xué)員獲得全國第三名。










