A-level數學課程知識點整理：導數中的乘法法則

微積分是A-Level數學課程中非常重要的一塊內容，歷年來也都是考察的重點所在，該內容在純數學一，純數學二，純數學三中都有涉及。今天帶大家來看A-level數學課程微積分中同樣非常重要的另外兩個法則Product Rule知識點整理。

求導法則共有三種：products rule（乘法法則），quotients rule（除法法則），chain rule（鏈式法則）。

乘法法則是在微積分中用來求一個由兩個或幾個更小的函數的乘積函數的導數，也就是說，函數f(x)可以看成g(x)h(x)的乘積形式。看看下面這些例子，你會有更好的感覺：

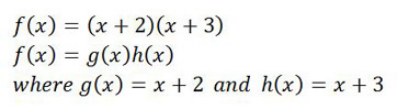
以上這個函數是由兩個更小的函數組成的乘積形式。有同學會不禁發問，考試只會考查由兩個函數組成的乘積嗎？

A-Level的考綱要求我們只用掌握兩個函數相乘形式的公式，但是會考查到多個函數相乘的題目，所以下面我們做一個額外補充，來看下面這個函數就是由三個更小的函數的乘積形式，公式會附在之后。

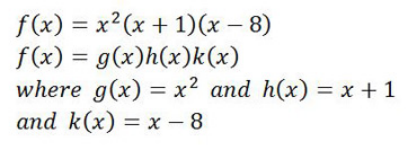
以下就是兩個函數乘積形式及三個函數乘積形式分別的公式：

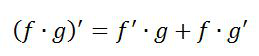
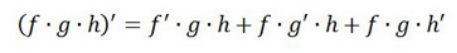
仔細比較這兩個公式，你們看到了每個函數是如何保持整個函數的，但是答案的每一項都是其中一個函數的導數嗎？

對于兩個函數的乘積，我們取第一個函數的導數乘以第二個函數然后將它與第二個函數的導數乘以第一個函數相加。

對于三個函數的乘積，我們取第一個函數的導數乘以其余的，然后我們將第二個函數的導數乘以其余的，然后我們將第三個函數的導數乘以其余的，以此類推。

你們知道如何對每個連續較小的函數求導同時保持較大的函數作為一個整體嗎？這里有一些例子來說明問題。

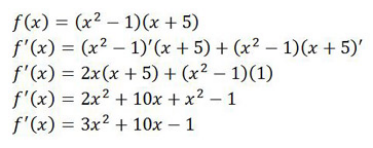
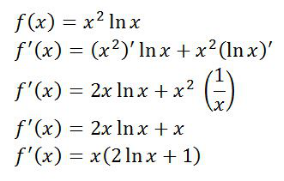
最后歸納總結，Product rule就是對乘法形式函數進行微分的方法。微積分是貫穿P1-P4的重點內容，大家一定要重點理解。

需要針對A-level考試輔導提升的同學可以掃碼添加翰林顧問老師咨詢~

還能【免費領取】相關真題及解析！