A-Level數學中導數的除法法則運用

數學是一門研究數字、數量、形狀、空間及它們之間關系等等的龐大學科，這門課有大量的領域和分支，是當今許多科學技術的基礎。數學一般分為純數和應用數學，前者研究的是完全抽象的對象，而后者關注的是數學在現實生活中的應用。

A-level數學將幫助學生理解基本的數學概念和思想，拓展計算技能和解決問題的能力，這些都是進入高等教育和未來職業生涯所必需的。今天我們分享的是A-Level數學中導數的除法法則運用。

和乘法法則類似，微分除法法則適用于求由兩個或幾個函數的商函數的導數，也就是對函數f（x）=g（x）/h（x）進行求導，或者表達為對y=u/v進行求導，其中u和v都是關于x的函數。

關于這類函數的求導，我們可以利用之前學習過的鏈式法則和乘法法則進行推導：

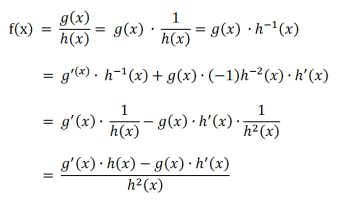
Step1：將函數改寫成便于求導的指數形式；

Step2：利用Product Rule和Chain Rule對函數進行求導；

Step3：整理函數，寫成分數的形式；

Step4：通分，將分母統一化成h2（x），得到最終結果。

總結：微分除法法則如下，可以寫成兩種形式：

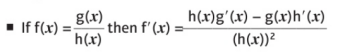
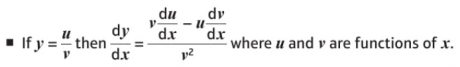
記憶的方法也和之前Product Rule類似，我們可以編個小口訣，“上導下不導，減去，下導上不導，整體除以下面函數的平方”。再結合之前的學習，無論這個分式方程的分子和分母是由多少個函數組成，我們都可以對式子進行求導。

Question 1：

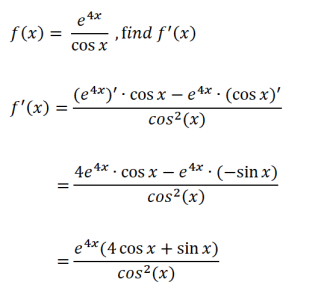
學會微分除法法則，分式求導是不是so easy，那么，下面我們稍稍提升點難度！

Question 2：

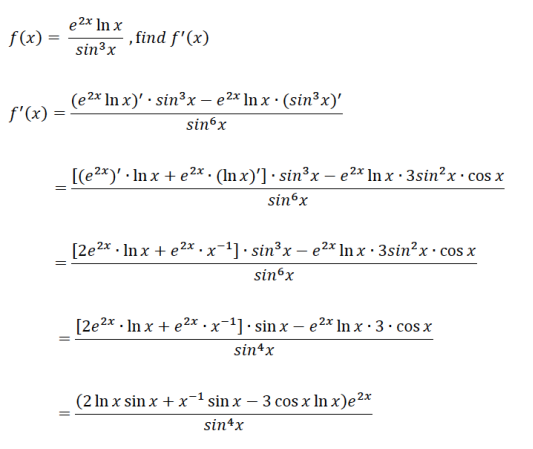
結合了微分法則三巨頭的題目還是有點難度吧，但只要掌握公式和方法，逐層運算，就可以輕松擊破。

最后，在P3的考試中我們見到的函數求導基本都會是將多重法則（Chain Rule,Product Rule,Quotient Rule）的綜合運用，大家一定要熟練掌握。

需要針對A-level考試輔導提升的同學，歡迎掃碼詳細咨詢~

還能【免費領取】相關真題及解析！