AMC10晉級AIME難度如何？晉級秘訣看這里

AMC10晉級AIME比例一覽

為了幫助大家更清晰直接地了解AMC10晉級AIME的比例，我們在MAA網站統計了相關數據，并為大家呈現出來。俗話說，知己知彼百戰不殆，只有清楚定位和差距，學習起來才更有目的性。

通過2012年至2021年秋季AMC10 A卷和B卷的DHR分數線及晉級AIME的比例（見下圖），不難看出，2020年以來的三次AIME晉級率較之前有了明顯的提升。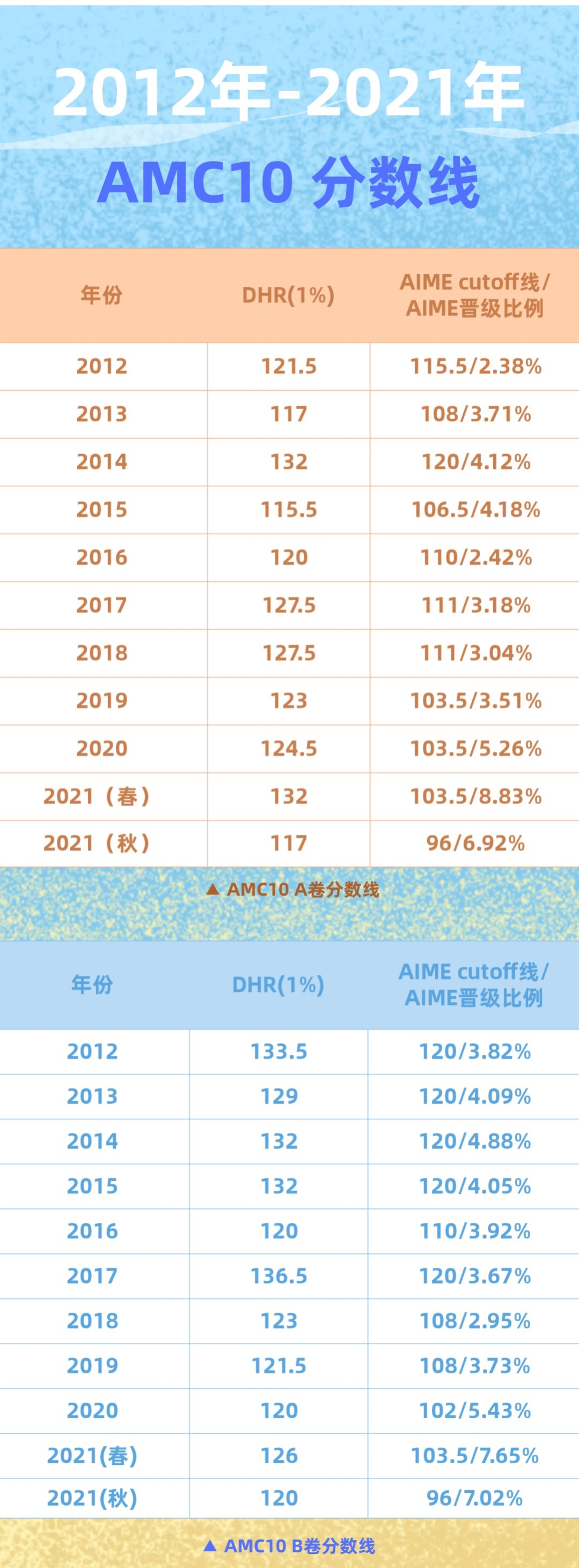AMC10 A卷晉級AIME的比例在2019年及之前始終處于較為溫和的上下波動中，2012年晉級率最低，為2.38%，2015年晉級率最高，為4.18%，差值為1.8%。但是，在2020年至2021年秋季的三場考試中，晉級率卻出現了較大的上漲，分別為5.26%，8.83%（歷年最高）和6.92%。

同樣地，AMC10 B卷晉級AIME的比例在2019年及之前也是處于少量的動態變化中，2018年晉級率最低，為2.95%，2014年晉級率最高，為4.88%，差值為1.93%。在2020年至2021年秋季的三場考試中，AMC10 B卷晉級率則出現了較大的上漲，分別為5.43%，7.65%（歷年最高）和7.02%。

AMC10 是什么？AIME又是什么？

了解完晉級比例，接下來，我們共同關注AMC10和AIME的基本信息介紹。

AMC10基本信息介紹
AMC10是美國高中數學學術活動中的一項，主要針對高一年級及以下學生，該學術活動開始于2000年，于每年的11月中下旬舉行。AMC10分A賽和B賽，難度相當，并無太大差異，且分數線分別制定，學生可任選一項參加。

AMC10學術活動的目的是通過在測試中解決富于挑戰性的問題，提高學生在數學方面的興趣及問題解決能力，學術活動內容為除去微積分以外的高中數學, 由于考題是為從一般學校的普通學生到重點學校的優秀生中的每一位而設計的，因此測驗范圍由易到難，雖然考題都很具挑戰性，但又在學生們力所能及的范圍內。因為考察能力及知識面的范圍很廣，因此考生的成績分布也很廣，通常獲得120分以上的考生比例較低。

AMC10的另一個目的是發掘一些在數學方面有才華的學生，讓校方能重視這些學生的存在，好的數學家就是這樣被發掘、鼓勵并獲得發展的。在AMC10活動中，如果排名在前2.5％，肯定會受邀參加美國數學邀請賽（AIME），實際錄取比例會更大一些。

當然了，學習 AMC10 可以為后續備考 AMC12 及 AIME 打下堅實基礎，是拿下更高獎項的一個好幫手。

AIME基本信息介紹

AIME 全稱American Invitational Mathematics Examination, 是介于AMC10、AMC12及美國數學奧林匹克學術活動（USAMO）之間的一個數學學術活動，學術活動開始于1983年，在每年的2月舉行，一共兩次，分為AIME I和AIME II。兩次考試和AMC10/12的A卷和B卷考試模式類似，難度和效力基本相同。中國考生只能選擇一場參加，一般參加AIME I 的考生居多。

AIME考題相當有難度，考生一般不能通過猜測得到正確答案．考試內容為除去微積分外的中學數學。與美國高中數學學術活動及美國數學奧林匹克學術活動一樣，考題都能用不超過微積分外的中學教學方法解決。AIME的目的是確定大學之前階段在數學方面杰出的學生，選拔美國數學奧林匹克學術活動的參加者。該考試可以為有數學方面優勢的高中生提供進一步挑戰并提供認識其才干的機會，而且它的實用價值在于考前的準備及考后對考題的進一步思考和討論。

美國就讀的考生如果可以在AIME活動中拿下好成績，還有機會參加后續的USAJMO和USAMO活動，這是更具含金量的數學賽事，絕對可以拿到簡歷上大夸特夸。

掃碼免費領取AMC資料包！包含近十年真題及解析！
領取報名表/咨詢報名注意事項/名師在線輔導！

AMC10晉級AIME的秘訣是什么？

縱觀往年，AMC10如果想要晉級AIME至少要排到前5%左右才算穩妥。如何脫穎而出？當然是刷真題、熟悉并掌握考點。通過查看自己不熟悉的考點并針對性進行真題訓練，考生才能有效查漏補缺，針對性提升，從而實現快速進步。




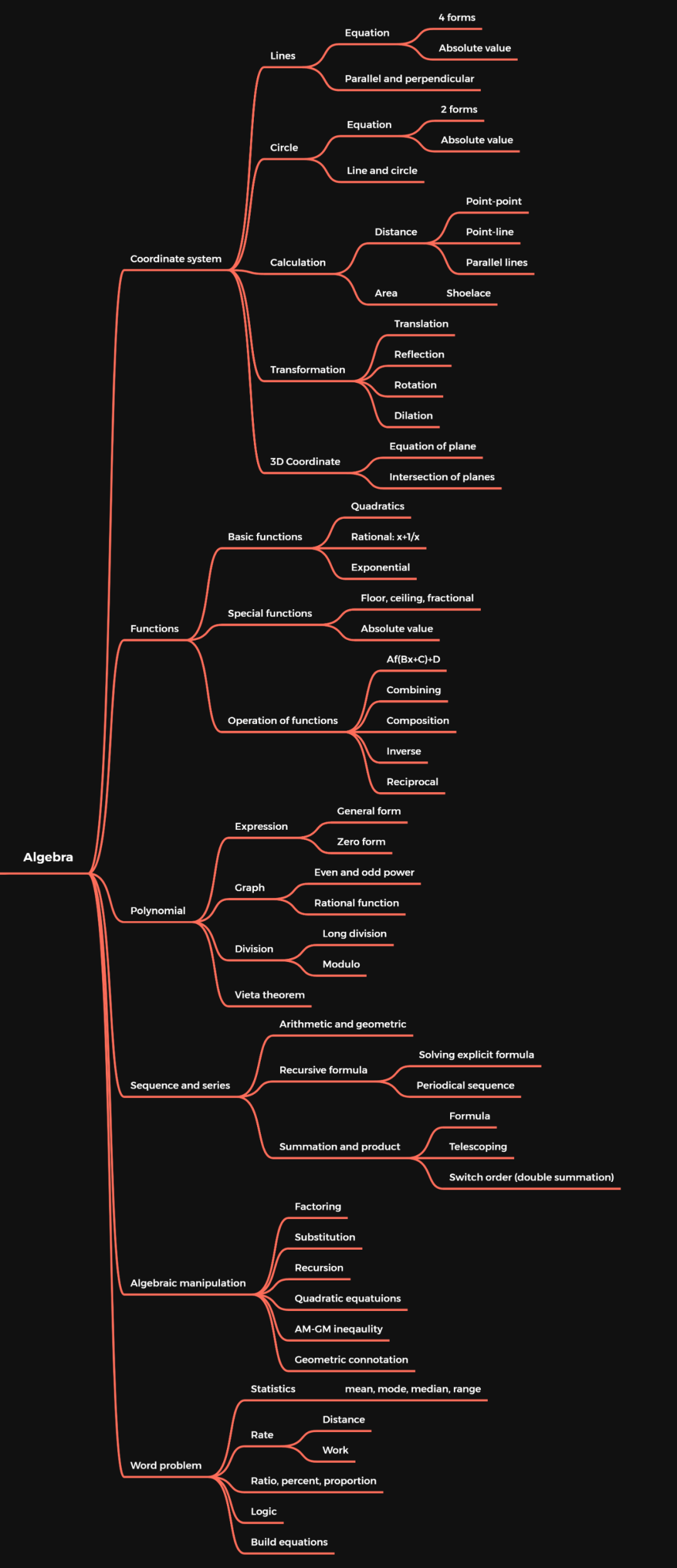
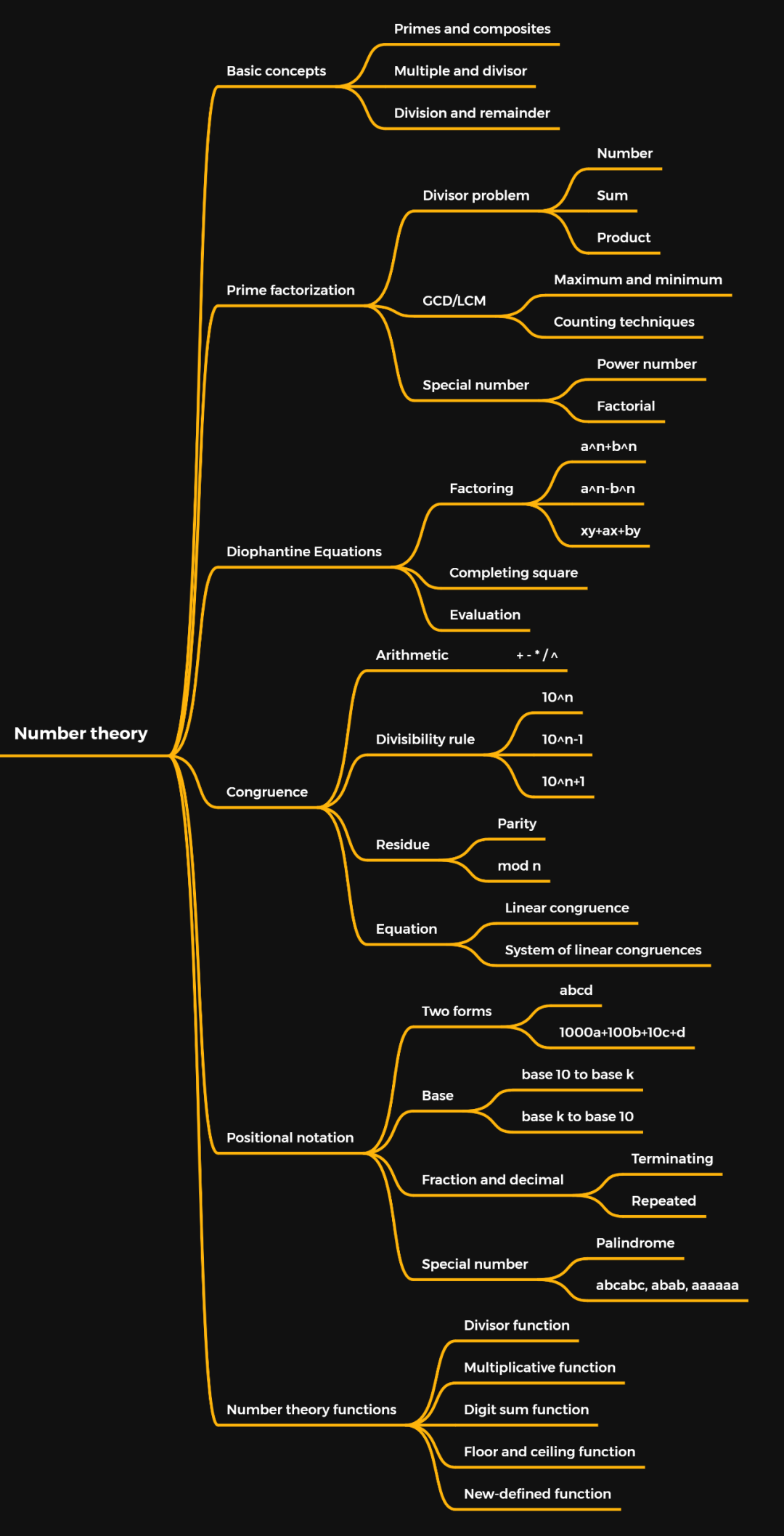
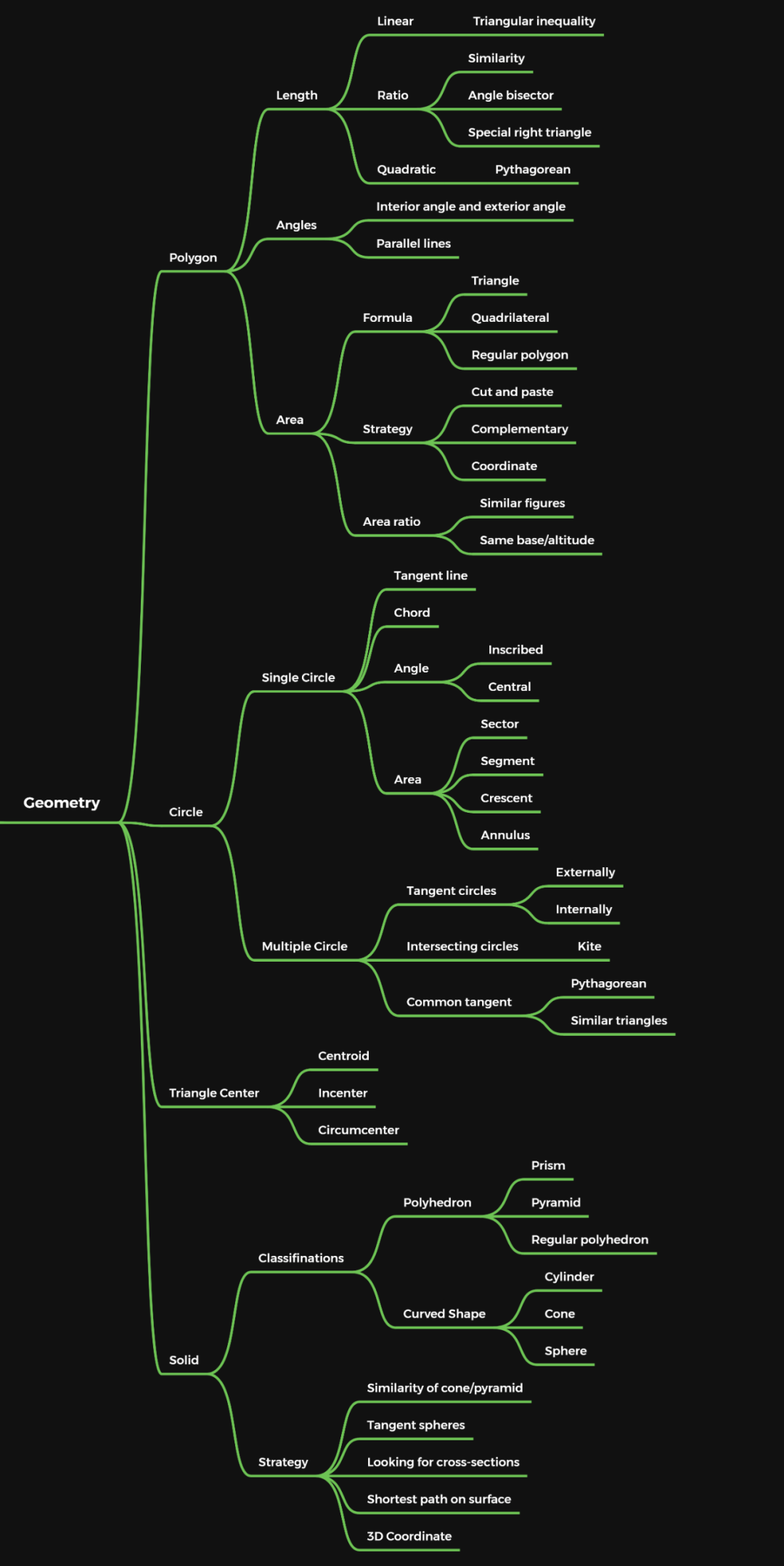
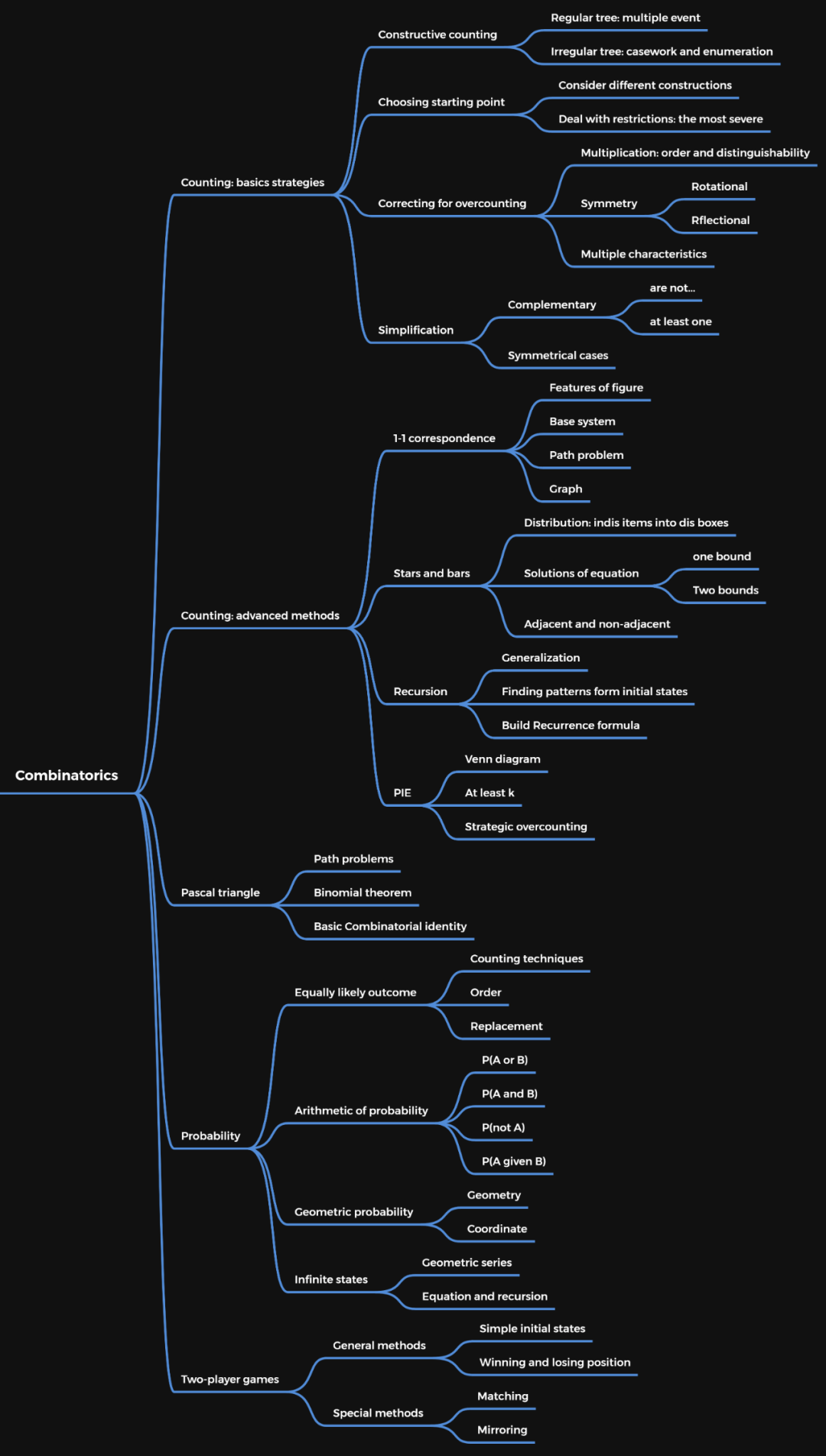
AMC10考點一覽

此外，我們參加AMC10一方面是熟悉AMC考試流程，提高數學興趣，另一方面，也是為進入AIME并在AIME考試中取得高成績做準備。所以，對于學習能力不錯的考生，降維打擊不失為一個好方法。通過練習AIME試題，訓練技巧，考生可以為AMC10做好充分準備。不過該建議并不適用于所有考生，大家量力而行哈。如果你覺得AIME試題過于困難，還是以打好基礎為首要任務。

AMC10和AIME的考察區別

差異一： 不同的考試形式
從75分鐘25題的選擇題（AMC10），變成3小時15題的填空題（AIME），巨大的考試形式的差異，這意味著我們不再可以用選擇題的答題技巧（如排除法、試數法、度量法等），而是要硬碰硬地去解決每一道題目。在相對比較充足的時間內，理解題意，聯系對應的知識點和技巧，通過一步一步地推理和計算，得到正確的結果。這非常考驗數學的基本功，也考驗心態和計算的穩定性。

差異二： 更多的知識點
AIME的大部分考點都是與AMC12一致的，此外在幾何、數論、組合模塊各多了少量的知識點，這些知識點大多比較復雜，一般出現在AIME的后5題中，掌握這些知識點是沖擊高分的關鍵。但是不要忘記前10題中，多數還是AMC10和12的核心知識點，因此鞏固強化AMC部分的內容也是很重要的。

差異三： 更加靈活和綜合的題目
AIME題目的最大特點就是靈活性、綜合性和多樣性。因此需要考生有很強的思維發散性，不要禁錮于某些刻板的公式和套路，而是真正去理解、思考、聯想，找到隱藏在眾多表面線索背后的本質。

? 靈活性：AIME里很多題目的考察不注重固定的知識點（性質或公式），而是背后的一些數學思想。例如代數部分，無論是對數題、三角題、復數題，都可能會考察一些代數變形的思想和技巧，如整體代換、因式分解、遞推方法、對稱式和輪換式、自相似、賦予代數式幾何含義等等。這些技巧都非常靈活，不是死記硬背就可以套用的公式，需要考生拿到題目時，進行思考、分析、嘗試，確定最合適的方法，然后再進行求解。

? 綜合性：AIME的很多題目都可能會涉及多個模塊的知識點，即涉及交叉領域的題目。例如一道三角函數的題目，可能會牽扯復數和多項式的技巧以及幾何的性質；一道幾何的題目，可能會用復數和坐標系的方法；一道代數的題目如果有很多整數的條件，可能會和數論有很大的關系；一道概率計算的題目，可能最終是一個遞推數列求解或者多重數列求和的問題。

? 多樣性：AIME的題目往往會有很多的切入點，也會有多種解法。例如一道組合題目，可能可以用分類討論加枚舉解決，可能可以用遞推進行計算，也可能用一一對應的方法一步解決。一道幾何題，可能可以用勾股和相似解決，可能可以用三角暴力計算解決，也可能用建坐標系的方法解決。因此越“多才多藝”的同學，在做AIME題的時候，越是能夠找到最合適的方法，提高自己的正確率。

其次，了解AMC10和AIME知識點差異也很重要。相較AMC10，AIME更多加入了以下知識點的考察：
? 代數：對數、三角函數、復數與單位根、多項式的根、圓錐曲線、三維坐標系、多重數列求和；
? 幾何：三角形的多心問題、根軸與根心、塞瓦定理（Mass point方法）、位似變換、圓冪、圓內接四（多）邊形、內心與圓外切四邊形、正余弦定理、 Stewart定理；
??數論：高次同余方程、指數型同余計算問題（費馬小定理與歐拉定理、LTE引理、階與原根相關定理）、線性不定方程、?中國剩余定理；
? 組合：無窮時間狀態的期望問題、標數遞推、生成函數計數、遞推計數、插板法