2022AP微積分BC北美卷FRQ已放出，附考情分析

各位AP小伙伴們好呀~2022年5月9日進(jìn)行的AP微積分BC考試已經(jīng)結(jié)束，本場(chǎng)考試為線下紙筆考試，CB官網(wǎng)已更新了2022AP微積分BC北美FRQ真題。

2022年AP微積分BC考試已經(jīng)結(jié)束，本次北美卷的考題從難度系數(shù)來(lái)看是非常常規(guī)，整體簡(jiǎn)單，考試的方式非常友好。完全延續(xù)了疫情發(fā)生前2015-2019年真題的題目風(fēng)格。在以往的真題中都可以找到類似的題目。

整體考試難度
本次考試對(duì)于完整刷過(guò)2015-2019年微積分題目的同學(xué)非常友好，今年的FRQ和往年的FRQ相比，基本上是一個(gè)模子里刻出來(lái)的。對(duì)整體微積分掌握到80%，就可以愉快的搞定這場(chǎng)考試，順利拿到五分。

FRQ知識(shí)側(cè)重
關(guān)于知識(shí)點(diǎn)的側(cè)重，在數(shù)學(xué)考試中，依然還需要具備一些知識(shí)辨析的能力，單純的記住知識(shí)點(diǎn)是沒(méi)有用的，畢竟數(shù)學(xué)考試是考察思維的考試。即便是相似的知識(shí)，但依然需要具備完整的知識(shí)邏輯和思考邏輯，需要一定的列式和應(yīng)對(duì)變化的能力，本次考試中可能會(huì)對(duì)同學(xué)們產(chǎn)生困擾的兩個(gè)點(diǎn)：

1.變限積分考察中沒(méi)有積分式，需要自己根據(jù)題干寫出積分式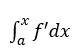，根據(jù)自己的積分式子進(jìn)行后續(xù)問(wèn)題的探討。

2.不同定理的考察，F(xiàn)RQ中需要對(duì)IVT&MVT&積分求平均值的方法進(jìn)行區(qū)分，特別是在原始信息已經(jīng)是rate的基礎(chǔ)上，這一點(diǎn)還是有一些難度。

掃碼添加翰林顧問(wèn)老師，可一對(duì)一制定國(guó)際課程規(guī)劃
【免費(fèi)領(lǐng)取】AP備考資料合集~

知識(shí)點(diǎn)與解題思路
總結(jié)而言，本次考試中的FRQ需要一定的數(shù)學(xué)思維能力，但是要求并不高。

FRQ 1：
本題考察的是積分應(yīng)用問(wèn)題
(a)問(wèn)是積分意義本身的考察，直接將速度進(jìn)行積分就可以得到數(shù)量。
(b)問(wèn)考察的是積分中值定理，將rate積分后除以時(shí)間跨度，可以得到平均數(shù)值。
(c)問(wèn)則是導(dǎo)數(shù)應(yīng)用單調(diào)性問(wèn)題，利用導(dǎo)數(shù)的正負(fù)判斷單調(diào)性。
(d)問(wèn)是導(dǎo)數(shù)應(yīng)用求最大值的問(wèn)題，對(duì)給定函數(shù)求導(dǎo)，借助計(jì)算器畫圖觀察導(dǎo)數(shù)圖像變化，借助導(dǎo)數(shù)圖像分辨單調(diào)性，由此獲得最大值得可能取值點(diǎn)，進(jìn)行互相的比較，獲得最大值。

FRQ 2：
本題考察的是二維運(yùn)動(dòng)問(wèn)題
(a)問(wèn)考察的是參數(shù)方程求導(dǎo)，直接利用參數(shù)求導(dǎo)公式運(yùn)算即可。
(b)問(wèn)考察二維速率，依然借助公式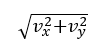獲得結(jié)果。
(c)問(wèn)考察位移問(wèn)題，對(duì)y方向速度積分后加上初始值即可。
(d)問(wèn)考察路程問(wèn)題，直接利用公式。

FRQ 3：
本題考察的是變限積分問(wèn)題
(a)問(wèn)以4作為起點(diǎn)，列出變限積分表達(dá)式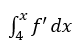，直接代值計(jì)算。
(b)問(wèn)已知f’圖像求拐點(diǎn)，根據(jù)f‘的單調(diào)性決定f’‘的正負(fù)變化，其中f’單調(diào)性發(fā)生改變的點(diǎn)即為拐點(diǎn)。
(c)、(d)問(wèn)直接將函數(shù)求導(dǎo)，得到g‘=f’-1，將給定函數(shù)圖像往下平移一個(gè)單位，進(jìn)行(c)、(d)問(wèn)的探究。

FRQ 4：
本題考察的是近似問(wèn)題
(a)問(wèn)考察近似求導(dǎo)的問(wèn)題，直接兩點(diǎn)聯(lián)立近似求導(dǎo)。
(b)問(wèn)考察介值定理，直接根據(jù)左右端點(diǎn)的數(shù)值進(jìn)行推斷。
(c)問(wèn)考察黎曼近似，取右端點(diǎn)的高度進(jìn)行面積計(jì)算近似。
(d)問(wèn)考察相關(guān)變化率，這個(gè)題目是雙變量的相關(guān)變化率，直接對(duì)表達(dá)式進(jìn)行求導(dǎo)，其中h與r的變化率都可以從題干中找到。

FRQ 5：
本題考察的是積分的幾何應(yīng)用
(a)問(wèn)考察積分求面積，直接在給定區(qū)域上進(jìn)行定積分求面積。
(b)問(wèn)考察定截面圖形求體積，利用積分公式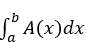，代入表達(dá)式進(jìn)行積分運(yùn)算，值得一提的是，這個(gè)題目進(jìn)行積分的時(shí)候需要使用分部積分法。
(c)問(wèn)考察反常積分的內(nèi)容，將給定面積的上下限定為3&∞，進(jìn)行正常積分計(jì)算即可。

FRQ 6：
本題考察的是泰勒級(jí)數(shù)
(a)問(wèn)考察的比值法，直接借助比值法公式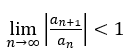，計(jì)算x的區(qū)間范圍。
(b)問(wèn)考察交替級(jí)數(shù)誤差，這個(gè)題目表達(dá)的相對(duì)隱晦，其中誤差是表達(dá)式第二項(xiàng)。
(c)、(d)問(wèn)直接對(duì)交替級(jí)數(shù)本身求導(dǎo)運(yùn)算即可，根據(jù)表達(dá)式進(jìn)行·求值。

整體而言，2022年北美卷試題考察的方式非常中規(guī)中矩，知識(shí)點(diǎn)也是以往考試的熱門知識(shí)點(diǎn)，如果單純進(jìn)行題目難度系數(shù)的橫向?qū)Ρ龋鸵酝攴莸念}目難度系數(shù)相差無(wú)幾。但是鑒于已經(jīng)有了前面年份的題目作為參考，在2022年面對(duì)這種相似的題目，可以說(shuō)是考察的更加簡(jiǎn)單了。