【A-Level物理】重難點(diǎn)解析 | 簡(jiǎn)諧運(yùn)動(dòng)（上）

首先我們來(lái)看什么是波動(dòng)（oscillation）：

Oscillation is a repeating back and forth movement on either side of an equilibrium position.

也就是說(shuō)，是圍繞一個(gè)平衡位置的前后運(yùn)動(dòng)，在我們蕩秋千時(shí)，最低的點(diǎn)，就是這個(gè)equilibrium position。

現(xiàn)在我們來(lái)看如何形容一個(gè)oscillation：

振幅（Amplitude）：the maximum displacement from the equilibrium position.

周期（Period）：the time taken for one complete oscillation.

頻率（frequency）: the number of oscillations per unit time.

相位（phase）: it describes the point that an oscillating mass has reached within the complete cycle of an oscillation.

相位差(phase difference)：the degree by which one oscillation leads or lags behind another oscillation.

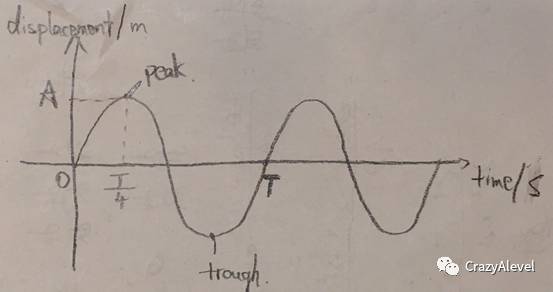
此圖為例，最高點(diǎn)叫peak，最低點(diǎn)叫trough，一個(gè)周期是一個(gè)完整的波動(dòng)所占用的時(shí)間（T）；

peak到橫軸的距離，就是最大的displacement，叫做amplitude；

頻率等于周期分之一（f＝1/T），單位為赫茲Hz，很多時(shí)候會(huì)用角速度ω（angular frequency），ω＝2πf，單位為radians；

至于相位，我們把一個(gè)完整的周期當(dāng)成2π，那么比如圖中的peak的相位就是π／2.

相位差呢，是針對(duì)兩個(gè)或多個(gè)波動(dòng)來(lái)說(shuō)的，兩個(gè)信號(hào)上同樣的點(diǎn)（比如兩個(gè)peak）之間的相位差就是兩個(gè)信號(hào)的相位差。

描述完波動(dòng)，我們來(lái)看簡(jiǎn)諧運(yùn)動(dòng)。

舉個(gè)例子：最經(jīng)典的，就是鐘擺，圍繞著中間的平衡位置一直波動(dòng)，那么這種波動(dòng)和普通的波動(dòng)區(qū)別在哪，滿足哪些條件才能被稱為簡(jiǎn)諧運(yùn)動(dòng)呢？

1. A mass that oscillates

2. A position where the mass is in equilibrium

3. A restoring force that acts to return the mass to its equilibrium position (the force is directly proportional to displacement from equilibrium position and directed towards the equilibrium position or a fixed point)

以上是滿足簡(jiǎn)諧運(yùn)動(dòng)的條件，很容易考到，尤其是第三點(diǎn)，在判斷是否是簡(jiǎn)諧運(yùn)動(dòng)的時(shí)候很重要，因?yàn)楹芏噙\(yùn)動(dòng)都可以滿足前兩個(gè)條件，所以一定要看使物體回到平衡位置的力是否是指向一個(gè)固定的點(diǎn)的，比如：

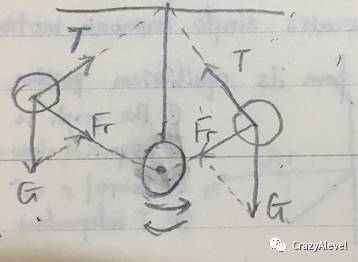
在這張圖中，運(yùn)動(dòng)的小球受到繩子的拉力T，重力G，在任何一個(gè)位置，受到的合力都是指向平衡位置的那個(gè)點(diǎn)的，所以這是個(gè)簡(jiǎn)諧運(yùn)動(dòng)。