2015COMC加拿大數(shù)學(xué)公開賽真題免費下載

歷年 Canadian Open Mathematics Challenge加拿大數(shù)學(xué)公開賽

真題與答案下載

 

翰林國際教育全網(wǎng)首發(fā)

力爭超快速發(fā)布最全資料

助你在升學(xué)路上一帆風(fēng)順

為你

千千萬萬遍

2015 COMC真題免費下載

共計2.5小時考試時間

此套試卷由三部分題目組成

4題簡答題，每題4分

4題挑戰(zhàn)題，每題6分

4題解答題，每題10分

共計12題，滿分80分

不可使用任何計算器

完整版下載鏈接見文末

部分真題預(yù)覽：

Part A Introductory Questions:

Question A2)In the picture below, there are four triangles labelled S,T,U and V.Two of the triangles will be coloured red and the other two triangles will be coloured blue. How many ways can the triangles be coloured such that the two blue triangles have a common side?

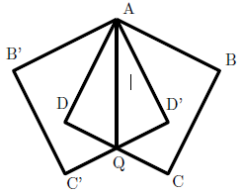
Question A3)In the given figure, ABCD is a square with sided of length 4, and Q is he midpoint of CD. ABCD is reflected along the line AQ to give the square AB'C'D'. The two squares overlap in the quadrilateral ADQD'. Determine the area of quadrilateral ADQD'.

Part B Challenging Questions:

Question B3)An arithmetic sequence is a sequence where each term after the first is the sum of the previous term plus a constant value. For example, 3, 7, 11, 15, . . . is an arithmetic sequence.

S is a sequence which has the following properties:

• The first term of S is positive.
• The first three terms of S form an arithmetic sequence.
• If a square is constructed with area equal to a term in S, then the perimeter of that square is the next term in S.

Determine all possible values for the third term of S.

Part C Long-form Proof Problems:

Question C4)Mr. Whitlock is playing a game with his math class to teach them about money. Mr. Whitlock’s math class consists of n≥2 students, whom he has numbered from 1 to n. Mr. Whitlock gives m_i≥0 dollars to student i, for each 1 ≤ i ≤ n, where each m_i is an integer and m₁ +m₂ +· · ·+m_n ≥ 1.

We say a student is a giver if no other student has more money than they do and we say a student is a receiver if no other student has less money than they do. To play the game, each student who is a giver, gives one dollar to each student who is a receiver (it is possible for a student to have a negative amount of money after doing so). This process is repeated until either all students have the same amount of money, or the students reach a distribution of money that they had previously reached.

1. Give values of n,m₁,m₂, . . . ,m_n for which the game ends with at least one student having a negative amount of money, and show that the game does indeed end this way.
2. Suppose there are n students. Determine the smallest possible value kn such that if m₁+m₂+· · · + m_n ≥ k_n then no player will ever have a negative amount of money.
3. Suppose n = 5. Determine all quintuples (m₁,m₂,m₃,m₄,m₅), with m₁ ≤ m₂ ≤ m₃ ≤ m₄ ≤?m₅, for which the game ends with all students having the same amount of money.

完整版真題資料可以底部二維碼免費領(lǐng)取↓↓↓