翰林國際教育,國內國際競賽領域的開拓者與引領者。我們不僅是系統輔導與深度教研的先行者,更為整個行業提供權威的賽事資訊與海量真題講義。在數學、物理、化學、生物、計算機、商科、數模等核心領域,我們的戰績長期穩居頭部領先地位,屢屢斬獲國家隊級別最高榮譽。作為同時擁有學科培訓、AP國際學校及美高資質的權威教育組織,我們為學生提供一站式的卓越培養體系,助力英才邁向世界頂尖學府。
AMC12與A-Level數學對比
一、 知識點重合與學習重點差異
1. ?核心重合領域分析
AMC12與A-Level數學在多個基礎數學領域存在顯著的知識點重疊,這為同時準備兩項考試的學生提供了協同效應的可能性。具體重合領域包括:
數列與級數:兩者都涵蓋等差數列、等比數列的求和公式與通項公式,但AMC12更側重數列的遞推關系、特殊數列性質及競賽級別的應用題
函數體系:包括多項式函數、指數函數、對數函數和三角函數的基本性質與圖像分析,A-Level側重函數變換與微積分應用,而AMC12注重函數方程與函數性質的深度挖掘
平面幾何:涉及三角形性質、圓形定理、多邊形特征等,AMC12的幾何題更具挑戰性,常結合多個定理綜合應用
概率統計:基礎概率計算、排列組合原理是共同內容,但AMC12的概率題往往情境更復雜,需要更強的建模能力
2. ?學習重點本質差異
A-Level數學:強調計算準確性和 procedural knowledge(程序性知識),要求學生能夠熟練執行計算流程,掌握標準解題方法,注重對數學概念的體系化理解
AMC12數學:側重數學思維的深度與廣度,考察學生發現模式、建立聯系、創新解題的能力,強調 conceptual understanding(概念性理解)和 strategic thinking(策略性思考)
3. ?互補性價值
兩項考試的結合能夠為學生提供更完整的數學素養培養:A-Level打下堅實的知識基礎和計算能力,AMC12則在此基礎上發展高階思維能力和問題解決技巧,形成"基礎+創新"的良性循環。
二、 考試性質與目標定位
1. ?AMC12:競賽導向的思維挑戰
核心目標:作為美國數學競賽體系的重要組成部分,AMC12主要旨在激發數學興趣、培養數學思維、發現和選拔數學人才
競賽特性:具有較高的難度和挑戰性,題目設計注重創新性和思維深度,考察學生在壓力下的問題解決能力
人才篩選:作為美國數學奧林匹克競賽(USAMO)的入門選拔,承擔著識別和培養數學尖子生的重要功能
全球影響:雖然源于美國,但已成為全球范圍內認可度極高的數學能力證明,尤其受到頂尖大學的重視
2. ?A-Level數學:學術導向的體系化考核
課程定位:作為英國高中課程的核心科目,主要為大學學習做準備,培養學生學術能力和專業基礎
教育功能:注重數學知識的系統性和完整性,強調為大學理工科、經濟科等專業學習奠定必要基礎
評估標準:采用學業水平考試模式,全面考查學生對基礎知識的掌握程度和應用能力
國際認可:作為國際通用課程,成績被全球大多數高等教育機構認可,是大學錄取的重要參考指標
3. ?價值導向差異
AMC12體現的是"精英教育"理念,追求數學能力的卓越性;A-Level數學體現的是"大眾教育"理念,確保數學素養的全面性。這種差異決定了兩者在難度設置、考查重點和準備策略上的根本不同。
三、 考試內容與能力要求
1. ?AMC12內容特點與要求
知識范圍:涵蓋代數、幾何、數論、組合數學等多個數學分支,內容廣度遠超常規課程
題目特征:
i. ?創新性強:多數題目為原創或改編題,避免機械刷題取得高分
ii. ?綜合度高:單個題目往往融合多個知識點,要求具備跨領域思維能力
iii. ?技巧要求:需要掌握特殊的解題技巧和方法,如代入法、排除法、估算法等
能力側重:
iv. ?快速解題能力:75分鐘完成25題,要求極高的時間管理和決策能力
v. ?邏輯推理能力:需要嚴謹的邏輯推導和證明能力
vi. ?創新思維能力:面對新穎問題時能夠提出創造性解決方案
2. ?A-Level數學內容特點與要求
知識體系:包含純數學、力學、統計學三大部分,內容系統全面
i. ?純數學:函數、微積分、三角函數、向量等核心內容
ii. ?力學數學:運動學、動力學、靜力學等物理相關數學應用
iii. ?統計數學:概率分布、假設檢驗、相關回歸等統計方法
題目特征:
iv. ?規范性強:題目設計符合課程標準,注重對教學內容的全面覆蓋
v. ?應用導向:強調數學在實際情境中的應用,特別是力學和統計部分
vi. ?證明要求:部分題目需要完整的數學證明過程
能力側重:
vii. ?計算準確性:強調計算過程的規范和結果的精確
viii. ?概念理解:要求深入理解數學概念的本質和內在聯系
ix. ?應用能力:能夠將數學知識應用于實際問題解決
四、 考試形式與評分體系
1. ?AMC12考試形式特點
時間壓力:75分鐘完成25道選擇題,創造極大的時間挑戰
答題策略:獨特的評分機制(答對6分,未答1.5分,答錯0分)要求精細的答題策略
題目順序:難度大致按題號遞增,但常有意外情況,需要靈活調整策略
全球統考:每年11月舉行,全球統一時間、統一試卷,確保公平性
2. ?A-Level數學考試形式特點
模塊化考核:分為多個單元考試,學生可以分階段完成
題型多樣:包含選擇題、簡答題和論述題等多種題型
時間分配:每個單元1.5-2小時,時間壓力相對較小
綜合評定:最終成績由各單元成績綜合計算得出
3. ?備考策略差異
AMC12備考:需要大量練習歷年真題,培養快速解題能力和特殊技巧,注重思維靈活性訓練
A-Level備考:需要系統復習課程內容,做好知識點梳理,注重計算準確性和規范性訓練
五、 教育價值與選擇建議
AMC12價值:
i. ?培養創新思維和問題解決能力
ii. ?增強大學申請競爭力,特別是理工科專業
iii. ?獲得國際認可的數學能力證明
iv. ?為參加更高層次數學競賽奠定基礎
A-Level數學價值:
v. ?建立完整的數學知識體系
vi. ?為大學專業學習做好準備
vii. ?獲得國際通用的學歷認證
viii. ?培養嚴謹的學術態度和學習方法
A-Level學生備考AMC12策略
一、發揮學科基礎優勢
A-Level數學為AMC12備考提供了堅實的知識基礎。學生在函數分析、微積分應用、概率計算等方面已具備扎實功底,這些內容與AMC12的代數、函數部分高度重合。備考時應首先鞏固這些優勢領域,確保基礎題型得分率。同時需注意,A-Level強調的計算規范性和過程完整性正是AMC12高分所需的基本素養,這一優勢應繼續保持和強化。
二、精準識別知識差異
AMC12包含大量A-Level課程未涉及的內容,這是備考的主要挑戰。重點需要補充的領域包括:數論基礎(整除性質、同余運算)、組合計數(排列組合高級應用)、幾何拓展(立體幾何、解析幾何深度應用)以及特殊函數性質。這些知識點需要系統學習,建議使用專業競賽教材,建立完整的知識框架。差異點的學習要注重概念理解而非簡單記憶,這正是AMC12的考查重點。
三、建立分階段備考體系
備考過程應分為三個階段有序推進:
1. ?基礎構建期(2-3個月):系統學習知識差異點,完成概念理解和基礎練習
2. ?能力提升期(2個月):通過專題訓練強化薄弱環節,培養競賽思維模式
3. ?沖刺模擬期(1個月):進行全真模擬訓練,提升應試能力和時間管理
每個階段都應設定明確目標,并通過定期測試檢驗學習效果。
四、強化競賽思維訓練
AMC12不僅考查知識掌握,更注重思維靈活性。備考時需要特別訓練:
● 多解法能力:對同一問題嘗試不同解法,培養思維發散性
● 快速判斷能力:通過題目特征迅速識別解題方向和難易程度
● 策略選擇能力:根據時間限制合理選擇攻堅或放棄的題目
● 驗算核查能力:建立快速驗算機制,避免低級錯誤
這些能力需要通過大量真題練習和反思總結來培養。
五、優化應試策略與心態
AMC12的獨特評分機制(答對6分、未答1.5分、答錯0分)要求特別的應試策略:
● 時間分配策略:前10題快速完成,中間10題穩扎穩打,后5題選擇性攻堅
● 風險控制策略:對不確定題目采取謹慎策略,避免盲目猜測
● 心態調整策略:接受不可能完成所有題目的現實,專注于得分最大化

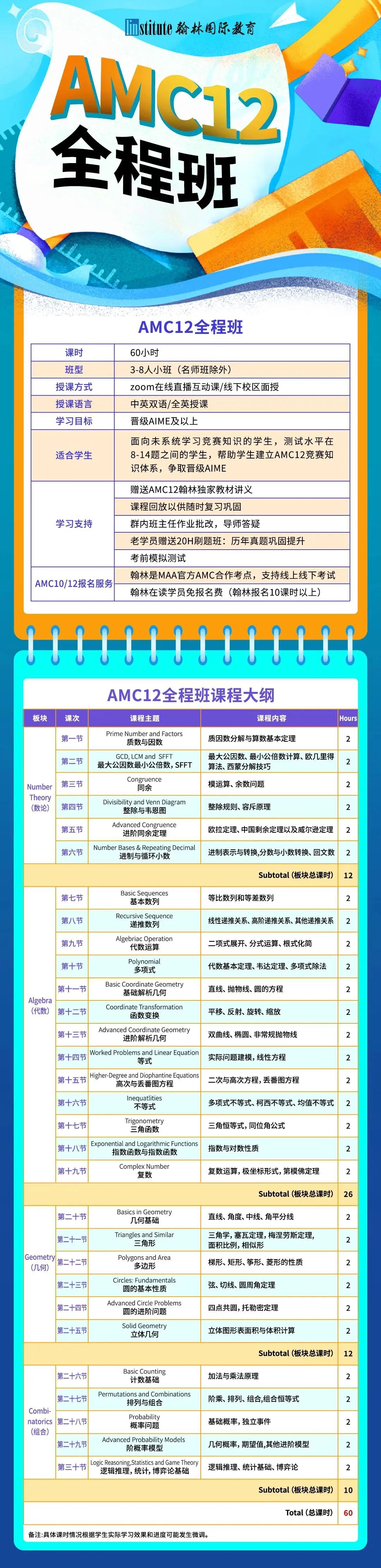
翰林AMC12競賽課程



翰林AMC12競賽課程