利用幾何變換解一類平幾最值問題

處理三角最值問題，在課堂教學中一般多利用基本不等式或建立函數結構來求，但往往運算量較大或設參數不明確,若能從幾何角度來思考問題，有時會有意想不到的收獲.下面我們從兩個問題出發來說明幾何變換在求平面幾何最值中的應用.

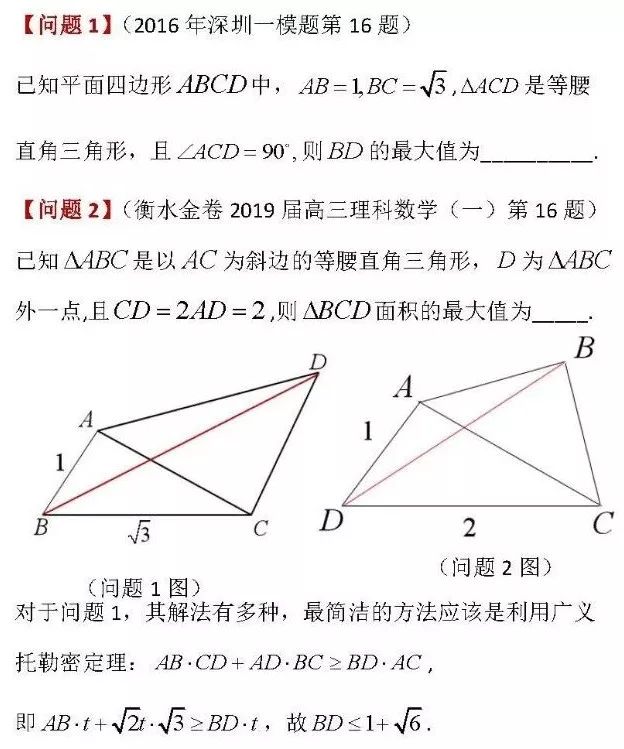
‍但上述方法對于沒有學術活動經歷的學生而言顯得過于高端，僅有結論而缺乏推導過程并沒有完整揭示這類問題的本質，比如我們要探究問題2中三角形BCD面積的取范圍時，托勒密定理的結論似乎就用不上，問題1和問題2“似乎”變成了兩個相對獨立的問題.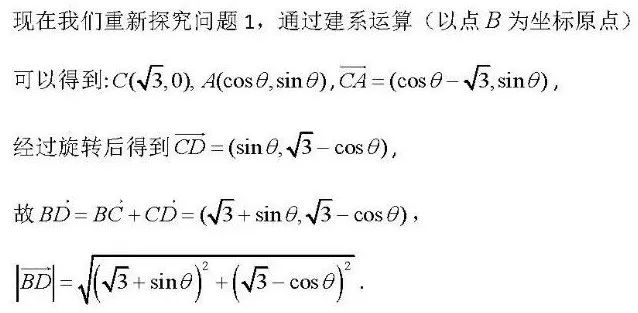

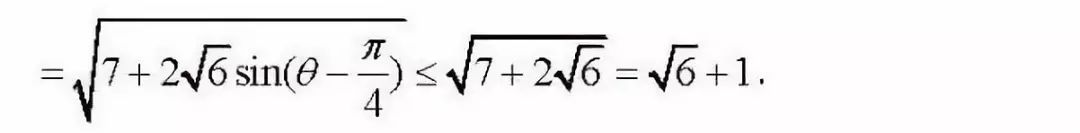
‍從上述代數推導過程中可以發現點D的軌跡應該是一個圓，但該推導過程中運算量會比較大，對學生要求較高，事實上，我們可以通過一個簡單的幾何圖形旋轉來說明為什么點D的軌跡是一個圓.

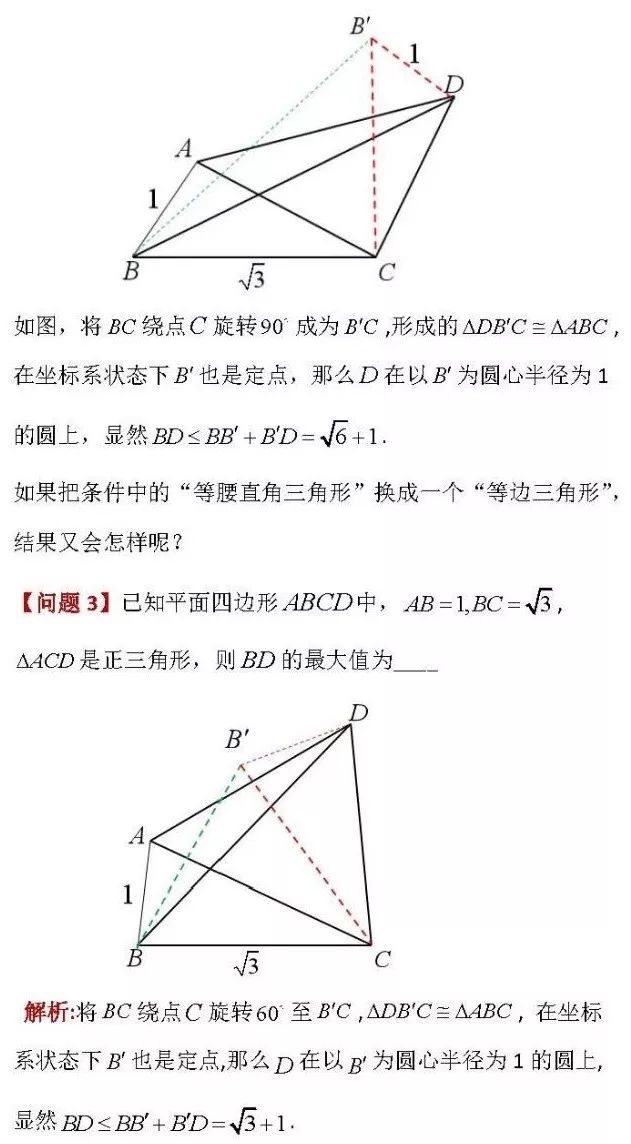
‍相比而言，純幾何途徑解決這個問題，明顯簡潔許多，當然該解法過程實際上也解決了例1中新增的那個問題，即本質上只需要搞清楚動點的軌跡是一個圓，那么長度和面積的最值解法本質是一樣的.

以上結果似乎表明，若ACD是一個相對特殊的三角形，用旋轉的方法（旋轉角度和特殊三角形相關）可以輕松得到BD的最大值和三角形面積的最大值，然而事實并非這么簡單，我們再回到問題2.

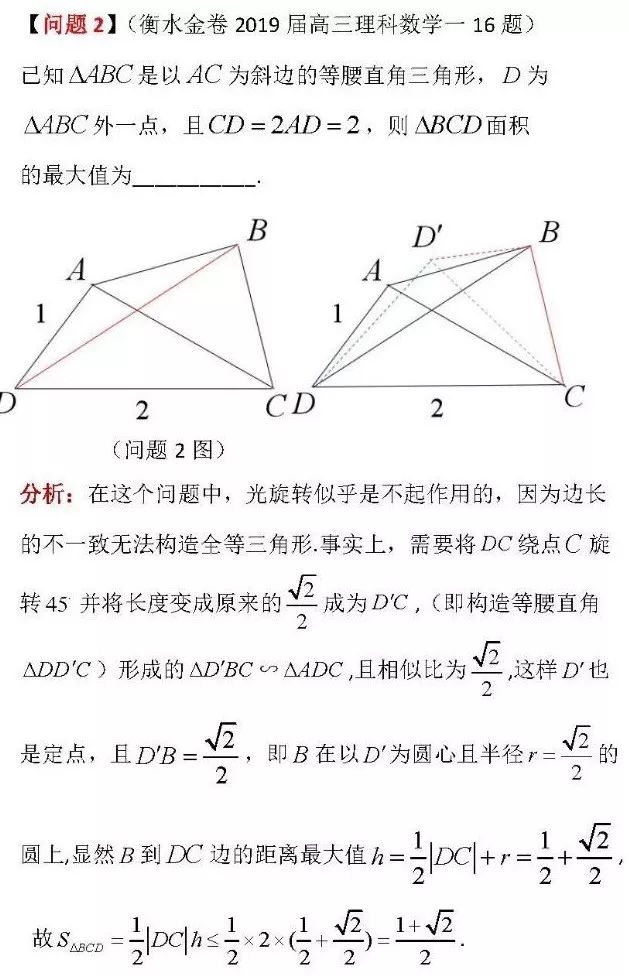
‍這樣我們就找到了解決這類問題的一般方法：利用構造局部相似三角形來解決問題，之前的全等構造實際上是此類問題中的一種特殊情況.

在更一般的情況下,利用上述構造相似三角形的思想可以相應得到：

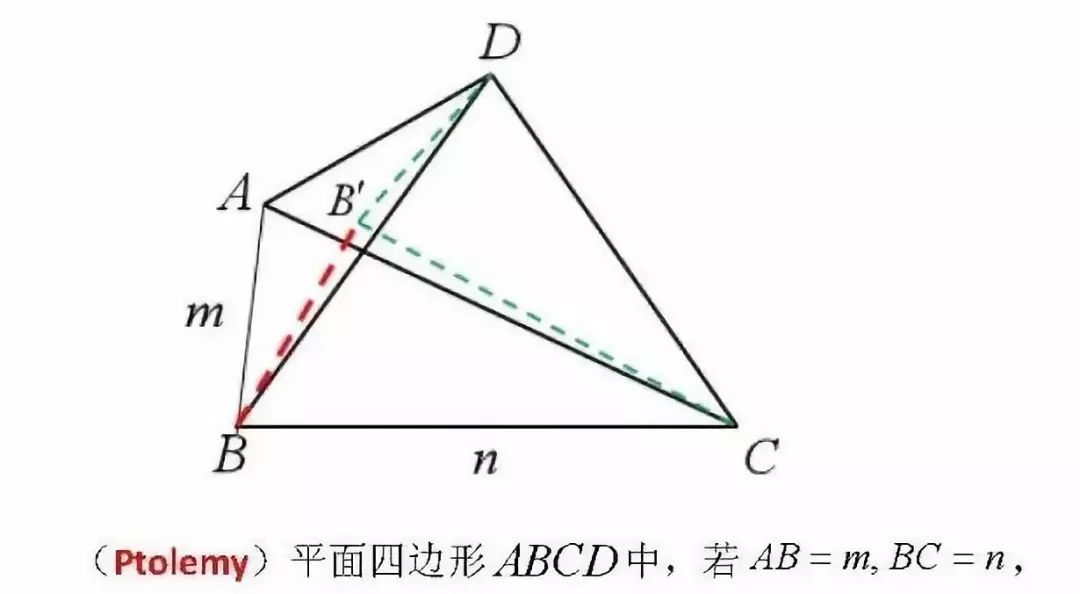
‍此結論即為廣義托勒密定理的基本結論，上述幾個例題的思考再現了這個經典的平面幾何定理的由特殊到一般的生成過程，顯然其中的思考過程比最終結論更有利于理解這類問題的本質，如伴生出來的面積最大問題，實際上考慮到三角形BCD的面積最大時，可能會造成A,B,C三點共線從而不能形成四邊形，故三角形BCD面積不一定有最大值（事實上，例題1中則三角形BCD的面積就沒有最大值），只能有一個取值范圍.

在這類三角最值問題的解決過程中，代數方向的思考會出現參數選擇的合理性、運算的要求高等諸多問題，而幾何方向的思考能體現一種解題的輕巧美，但是往往不容易想到，產生這一問題的原因在于初中教材對平面幾何能力的要求過低，而高中現在因為取消了幾何證明選講這個考點導致教師在教學上重視不夠，個人覺得很可惜，在建立幾何思維的道路上，平時的積累和總結很重要。另外，從代數推斷出的結論中多問自己為什么會是這樣，能否有幾何的解釋方法，保持對幾何的一顆好奇心，也是研究幾何問題的一個良好方法.