別人家學校的期末考試：一次函數難不難？

初中數學什么最難？ 一次函數來領銜！

是不是大吃一驚， 一次函數y=kx+b？ 除了正比例函數y=kx外，沒有比它更菜的了。

先看看數學課本的題目是怎么樣的？

已知點A（-1，a）和B(1,b)在函數y=-2x+m 的圖像上，試比較a與b的大小。

乍一看三個未知數a,b,m很嚇人，仔細一看該函數是單調遞減的，自然a>b.輕松搞定，一點都不難！

實際上，一次函數在平面直角坐標系中表示一條直線，它是代數和幾何的橋梁，把兩者結合起來，很容易出中考的壓軸題或者更難的名校自主招生題 甚至學術活動題。

先來一道簡單的熱熱身。

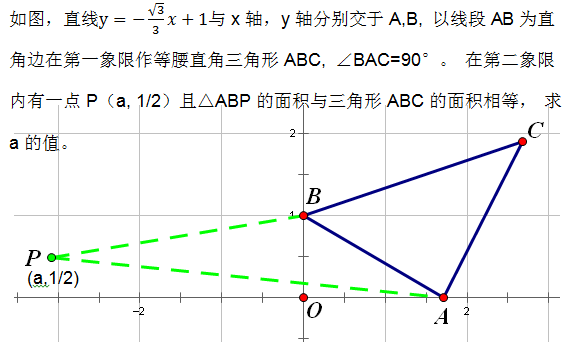
易知AC=AB=2， 且△ABP與△ABC共底邊AB，因兩個三角形面積相等， 故頂點P到底邊AB的高也為2. 如圖，

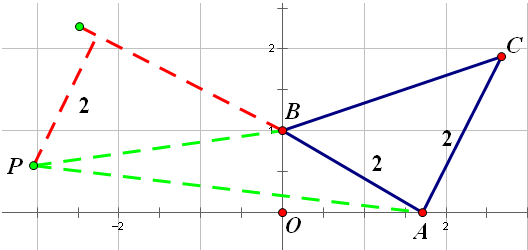
如果使用點到直線距離公式， P點的坐標立刻就能求出來了。

不幸的是， 這個公式是高中課本的內容，如果出現在初中答題卷上，除非自己從頭推導一遍，不然是一分不得的。

來看看如何用初中所學的內容求解。

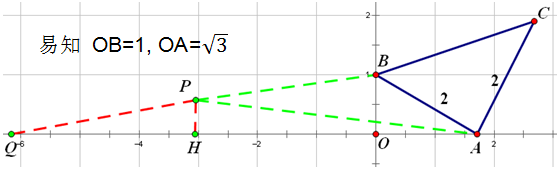
如下圖，延長BP交x軸于點Q,
∵P點坐標（a,1/2） ∴PH=1/2=OB/2
所以QH=OH=|a|,
S△ABQ= AQ * OB /2 = AQ/2
S△APQ= AQ * PH /2 = AQ /4
2=S△ABP= S△ABQ - S△APQ =?AQ /4
∴ AQ =8.

再來看看一道填空題：

在平面直角坐標系中，y=0.5x - 6分別與x軸，y軸交于A,B兩點。F(6,0)在x軸上，P，Q是線段AB上的兩個動點， 如果△OPF ≌ △OPQ, 求P點的坐標。

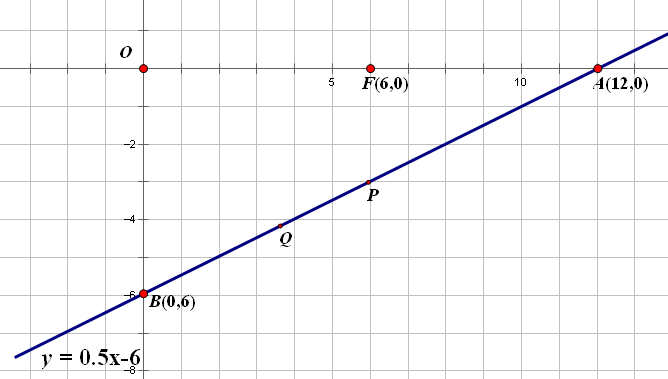
由△OPF ≌ △OPQ可得，OQ=OF=6, ?可以得到滿足條件的兩個Q點，其中有一個Q點和B點重合。

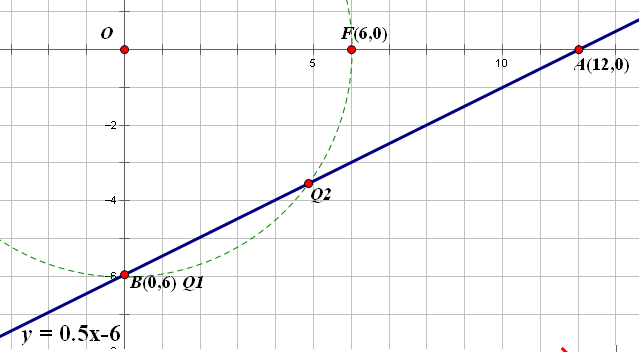
當Q點和B點重合時， 由∠POF=∠POB可以得到P點在y=-x上。

再聯立方程y=0.5x-6， 易知P坐標為（4,-4）.

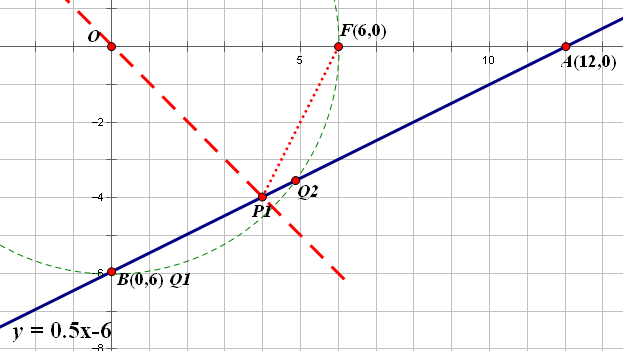
再看另外一個Q點， 根據兩點之間距離公式， 由OQ=6,可以得到Q點坐標。
再由PQ=PF，可以解得P點坐標。這是代數解法。

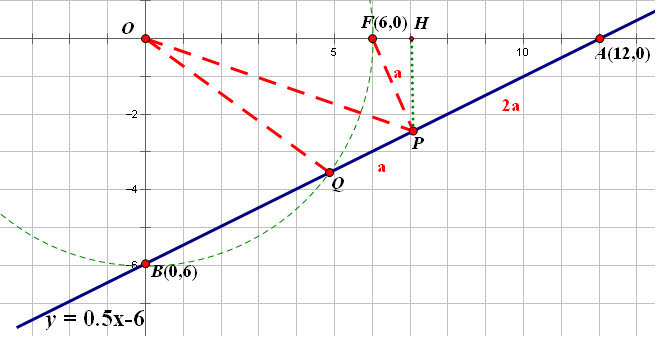
幾何解法也很有趣， 因為OP是∠AOQ的內角平分線， 根據內角平分線定理，
PQ: PA = OQ : OA = 6 : 12 = 1 : 2
又PF=PQ, 所以AP=2PF.
易知△APF 相似于 △AOB, ?所以PF⊥AP.
Rt△APF中， 知道了斜邊為6， 兩直角邊互為1:2， 高PH很容易求出來了，P點的坐標迎刃而解了。

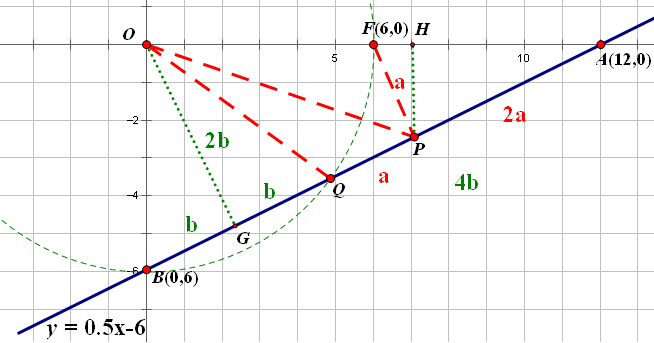
再舉一反三，我們會發現P，Q兩點分別在線段AB的2/5, 3/5上！！
作OG⊥AB， 易知△OBG 相似于 △AOG?相似于△ABO,
若BG =b, 則 OG =2b, AG = 4b = 3a +b.
所以a=b, 很神奇吧！

再來一道綜合題：

如圖，在平面直角坐標系中，直線y=x+2分別交x軸，y軸于A,B兩點， C為A,B的中點。D是線段OA上的動點，|OD|<1, 連接CD并將CD繞D點順時針旋轉90°至DE， 交y軸于F點，過E點做x軸平行線交AB于G點。 求四邊形BEFG面積的最小值。

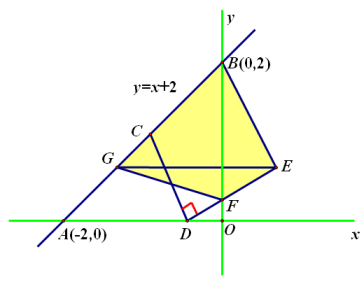
動點，旋轉， 極值問題？ 是不是有點暈？

下面是解題大概思路，

顯然，EG⊥ BF, 四邊形的面積等于(EG*BF) /2.
另∠A=45°， OA=OB=2. CD ⊥且 = DE
做垂線CM,EN，易知△CMD ≌ △ DNE

DN=CM=AM=1
令OD=m, ON=DM=1-m, EN=DM=1-m
所以∠EON=45°。 故OE//AG, EG=OA=2
相似三角形， DO: OF=DN:NE=1:(1-m)
所以OF=m(1-m), ?當m=1/2時取最大值1/4
此時BF取最小值7/4, 四邊形面積取最小值 2* 7/4 /2=7/4.

一道題綜合了初中數學代數、幾何的多個知識點，同學們可以自己梳理一下