2022年AMC8來臨，掌握這5大思維法，助你攻克AMC排列組合！

在AMC8的考試中，除了有一些可以通過直接計算快速得分的題目，又有一類則是專門用于對學生進行能力分級的題目。而這類題目經常出現在統計學中的排列組合，概率，幾何學中的面積體積計算，函數中的特殊符號計算與推理，以及代數中的計數知識點中。

這些知識點的學習都需要一定基礎。比如在一般的數學學習體系中，排列組合是在高中階段才會碰到的知識，并且在AMC考試中還進行了適當的加強，因此是當之無愧的難點知識。

今天就帶大家來梳理5大類排列組合的題型以及對應的計算方法，助你徹底攻克這一AMC知識難點。

1.表格法（Counting Using Charts）

在做計數原理的問題時，窮舉法都是一個不錯的方法。當我們把所有的情況羅列出來的時候，問題就會變得清晰直白。而羅列情況時，比較好用的是表格法和樹狀圖法。其中表格法是出現在兩個獨立的試驗中的情況，例如下題：

Exampie8.Two dice are rolled. How many ways are there to roll a sum of 5?

當出現兩個獨立的事情同時發生的時候，我們可以將兩個事情發生的所有情況分別放在表格的第一行和第一列上（如下圖所示），此時這個6*6的表格中的數據，就對應事情發生的所有情形。

而在表格中的數據也變得一目了然，如題干要求中尋找和為5的情況，便可以直接讀出有四種可能性。

2.樹狀圖法（Counting Using Tree Diagram）

當出現超過兩個事件的情況，表格法便失去了效果，此時就可以采用樹狀圖法。當然樹狀圖法也適用于兩個事件的情況，它的應用能力比表格法要更加強大。樹狀圖法是指將事情分為幾步，然后在第一步發生的情況下考慮對應的分支情況。

例如下面這道題，選擇有多少種方案可以搭配裙子。第一步可以選擇顏色，顏色的情況有三種，第二步則是在不同顏色的基礎上選擇款式，每一種顏色下對應著四種款式，因此應該是3*4=12，選C。

Example 9.A designer has 3 fabric colors he may use for a dress: red, green,and blue. Four different patterns are available for the dress. If each dress design requires one color and one pattern, how many different dress designs are possible?

(A)10 (B)24(C)12(D)14 (E)20 P2

同時如果將這個題目難度系數提高，在不同款式下還可以分為不同的型號，S，M，L。便可以在每個款式后面再分一個樹狀圖，最后的結果是3×4×3=36種。

3.捆綁法（Counting with restriction）

在排隊問題中，經常會碰到A與B想要靠在一起的情況，而遇到這樣的問題，又該如何計算其中的情況數。其中比較好用的方法為捆綁法，即先將想要靠在一起的人捆綁在一起視為一個整體，而后在進行排列。

Example 12.In how many ways can 5 books be arranged on a shelf if two of the books must remain together, but may be interchanged?

(A)12 B)24 (C)48 (D)96 (E)5

如上題所示，五本書進行排列但必須有兩本書靠在一起。大膽的操作一下，可以直接將這兩本書粘起來成為一本厚書，由此可以直接當作四本書在進行排列，總情況數為4！，但是兩本書粘起來的時候并不一定誰在左誰在右，因此其中有兩種情況。總的情況數應該是兩個數值相乘，即為4！*2=48，選C。

4.圓桌排列法（Circular Permutations）

圓桌排列是指當被排列的人并不是一條長列，而是考慮坐在一個圓桌上的情況數。圓桌排列與常規排列的區別在于——對于一個圓形而言，只考慮相對位置。例如有ABCD四個人坐在圓桌上，常規排列中的ABCD，BCDA，CDAB，DABC當出現在圓桌上的時候會被視為一種情況，因為四人的相對位置是不變的。因此在處理圓桌排列的時候總情況數應該為4！/4，因此可以直接記作3！。而對于n個人的圓桌排列可以直接記作（n-1）！。

THEOREM 3: The number of circular permutations (arrangements in a circle) of n distinct objects is (n - 1)!.

比如而對于下面的例題18這個題可以直接得到7個人的圓桌排列情況數應該是6！。

Example 18.In how many ways is it possible to seat seven people at a round table?

5. 分配法（Combinations with Repetitions）

在AMC8中經常會出現這樣一種題目，小明手上有18個蘋果，如果要想將18個蘋果分給三個人，而必須保證每個人手上至少有一個蘋果，那么總共有多少種情況？

這一類問題可以直接用分配法的公式進行直接計算，對于這樣一類問題，可以直接使用下面的公式，即為：
THEOREM 4:Let n be a positive integer. The number of positive integer solutions to X1+X2+…+Xr=n is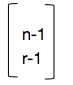
對于上述的分蘋果問題，可以直接列式。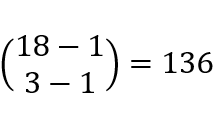
而如果對問題進行升級，同樣還是分蘋果的問題，但是不用保證每個人手上至少有一個蘋果，則可以直接利用下面的公式：

THEOREM 5:Let n be a positive integer. The number of non-negative integer
solutions toy1+y2+…+yr=n is
對于新的分蘋果問題，則可以直接寫作。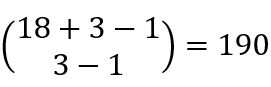

在2019的AMC8的考試中，最后的壓軸題就是考察的分配法的問題，這個題在上述公式基礎上可以適當進行發散就可以做出來。
Problem25

Alice has 24apples.In how many ways can she share them with Becky and Chris so that each of the people has at least 2apples?
(A)105 (B)114 (C)190 (D)210 (E)380

如上題所示，24個蘋果分給三個人，每人至少有兩個蘋果，其實相對于先分出六個蘋果，剩下的18個蘋果分給三個人并不用保證每個人的手上有蘋果，總情況數為。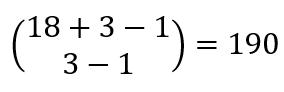

以上就是在AMC 8中經常出現的排列組合類型，在這種題目中，運算不是最重要的，重要的是思考問題的方式。只要思考的方向準確，通過一個算式就可以得到最后的結果，但如果思考不清晰，那便可能思慮很久也得不到有效的結果。

為了幫助同學們吃透排列組合問題，翰林精心準備了習題集給大家，幫助大家鞏固這幾種方法，大家可以檢測一下自己是否掌握了上面這些方法。AMC8學術活動來臨，有需要的同學掃碼即可免費領取~

 

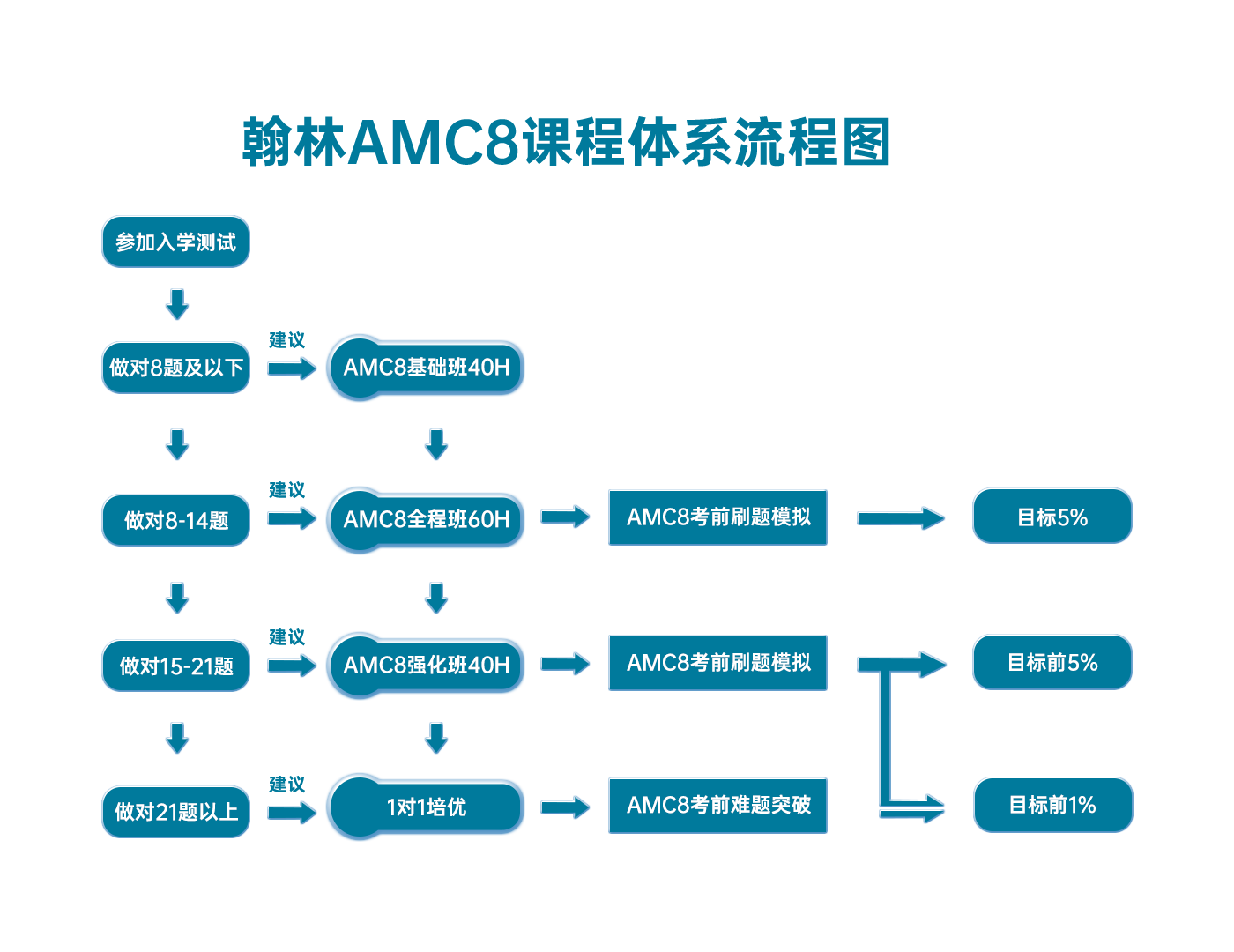
翰林AMC8課程體系流程圖